In the beginning, we studied the geometric elements of a Euclidean space in complete absence of
coordinate systems. In recent chapters, however, in an effort to increase the analytical power of
our framework, we introduced coordinates along with the most crucial elements of the tensor
notation. We will now put all of this together and begin to study the key coordinate-dependent
elements of a Euclidean space.
9.1Coordinates and the position vector function
We have already encountered the position vector , also known as the radius vector, which points from an
arbitrary fixed origin to each point in the Euclidean space.
The purpose of the position vector is, of course, to represent the position of the corresponding
point by an object that is subject to analytical operations. Every one of our geometric analyses
will start with the position vector. However, despite its fundamental role, it will rarely figure
explicitly in advanced stages of most of our analyses, as we will be more interested in its
derivatives rather than the position vector itself. This is part of the reason why the origin can be selected arbitrarily: its
location has no bearing on the derivatives of .  (9.1)
(9.1)
 (9.1)
(9.1)The position vector is a vector field, since to every point in space, there corresponds a
particular value of . However, as you see from the above figure, it is usually
depicted in an unusual way compared to most vector fields. For most vector fields, such as the
velocity distribution of a fluid, we usually imagine vectors emanating from the associated points
in the Euclidean space, as in the following figure from Chapter 4.  (9.2) The position vector, on the other hand, is best imagined
emanating from the origin , as you see in the preceding figure.
Because of this unconventional representation, we need to remind ourselves that the position vector
is associated with the point to which it is pointing, rather than the origin.
(9.2) The position vector, on the other hand, is best imagined
emanating from the origin , as you see in the preceding figure.
Because of this unconventional representation, we need to remind ourselves that the position vector
is associated with the point to which it is pointing, rather than the origin.
 (9.2)
(9.2)Now, impose a coordinate system upon the Euclidean space. Assume that the Euclidean space is
three-dimensional and, as usual, denote the coordinates by ,
, and
or,
collectively, .
Importantly, the coordinate system is assumed to be completely arbitrary as long as it is
sufficiently smooth in the sense described below. If the coordinate system has the concept of the
coordinate origin -- as most of the standard coordinate systems do -- it need not coincide with the
origin that anchors the position vector
field . We also remind the reader that the decision to use a
superscript to enumerate the coordinates is completely arbitrary in its own right. However,
once the decision to use a superscript to enumerate the coordinates is made, the placement of
indices on all subsequent objects is uniquely prescribed by the rules of the tensor notation.
In the absence of a coordinate system, the position vector is described by the term field
rather than function. A field is an association between the points of a Euclidean
space and some quantity. As such, the position vector is an example of a vector field.
Meanwhile, the temperature distribution in a room is an example of a scalar field. The term
function, on the other hand, describes an association between sets of numbers and
some quantity. Thus, with a coordinate system imposed upon the Euclidean space, we may begin to
speak of the position vector function
This function maps triplets of
numbers to
the value of the position vector at the point with coordinates ,
, and
.
By smoothness of the coordinate system we understand the differentiability characteristics
of the function . For most analyses, existence of second
derivatives is sufficient. We will often describe as sufficiently smooth, meaning that as
many derivatives are available as required by the analysis at hand.
As we have similarly noted in a number of analogous contexts, the symbol in the expression is being used in a new capacity compared to the
symbol in the absence of coordinates. In the absence of coordinates,
denotes a vector field, i.e. an association between
points and vectors. In the expression , however, denotes a vector-valued function of the three independent
variables ,
, and
. This
is another example of assigning the same symbol two closely related, albeit different, meanings.
From this point forward, we will collapse the functional arguments of all functions of
coordinates into the symbol . For example, the function will be denoted by the symbol
In addition to its compactness, the
symbol has the advantage that it works in any number
of dimensions. The alternative symbol cannot be used since it makes the index appear live and leaves it hanging, which violates the
rules of the tensor notation.
The function is the starting point for a crucial sequence
of definitions. Before we turn our attention to those definitions, it is important to reiterate
that the position vector is a primary object that is to be understood and
accepted on its own geometric terms. It is counterproductive to imagine some a priori basis
with respect to which could be represented by its components. There is simply no
such basis available -- nor is one needed.
9.2The covariant basis
9.2.1A note on the overloaded use of the letter
The remainder of the objects introduced in this Chapter are denoted by symbols anchored by the
letter . This includes the covariant basis
, the
covariant metric tensor ,
the volume element ,
the contravariant metric tensor ,
and the contravariant basis .
Despite the fact that the same letter is used in each of these symbols, they can be easily
distinguished by their indicial signatures. Additionally, the symbol for
the contravariant basis is distinguished from the symbol
denoting the coordinates by the fact that the letter is textbf{bold} in the former and
plain in the latter.
9.2.2The definition
The covariant basis , , -- or,
collectively, -- is
a generalization of the affine coordinate basis , , to curvilinear coordinates. It is constructed from the
position vector by differentiation with respect to each of
the coordinates, i.e.
Of course, the vectors , , and
constitute a legitimate basis only when they form a linearly independent set. Points where this is
not the case are called singular and almost always require special treatment.
As we have already discussed on several occasions, the term covariant describes the
placement of the index as a subscript and, correspondingly, the manner in which the basis
transforms under a coordinates transformation. For the time being, we will use the term
covariant without exploring its deeper meaning. Also note that, in reference to , we
will frequently drop the term covariant and refer to simply
as the basis.
It is not surprising that the first new fundamental object in a Euclidean space is introduced by
means of partial differentiation with respect to the coordinates .
After all, it is just about the only interesting operation that we have at our disposal that can be
applied to . Furthermore, it is remarkable that the
generalization of the coordinate basis from affine to general coordinates is accomplished by such a
simple operation. Just like that, we are able to decompose vectors, and thus conduct component
analysis, in general coordinate systems. Keep in mind, however, that -- unlike the coordinate basis
, , in affine coordinates -- the covariant basis varies
from one point to another and therefore the component space is specific to each point in space. As
a result, we must imagine an independent linear space at each point and work out how each space
interacts with the neighboring spaces. In the near future, we will have a lot to say about this.
Since we have decided to represent the function by the symbol , the definition of the covariant basis can be
expressed by the more compact equations
With the help of the tensor
notation, the above definitions can be combined into a single indicial equation, i.e.
The fact that the covariant basis ends up with a subscript illustrates an important feature of the
tensor notation which we have mentioned earlier on a number of occasions. Namely, that by strongly
suggesting the proper placements of indices, the tensor notation tends to predict the manner in
which objects transform under coordinate transformations. For the covariant basis , the
subscript is a natural choice since, as we discussed in Chapter 7, in the expression
the index appears as a superscript in the "denominator". Thus, the
tensor notation predicts that the covariant basis transforms in a manner opposite of the
coordinates. In Chapter 6, we have already observed
that this is the case for transformations between affine coordinates. For general coordinate
transformations, this will be confirmed in Chapter 14.
The covariant basis is
used for the decomposition of vectors at a given point. When a vector is decomposed with respect to , the
resulting coefficients are naturally assigned superscripts, i.e.
in order to utilize the summation
conventions in the equation
The components of a
vector with respect to the covariant basis are
referred to as the contravariant components. Of course, the broad goal of our analysis is to
replace vectors with their components so that we are able to solve problems by analytical rather
than geometric means. Thus, a detailed discussion of the components of vectors and their use will
be postponed until the next Chapter devoted entirely to coordinate space analysis.
Finally, note that it is not advisable to decompose the elements of the basis
itself with respect to some a priori supplementary basis. Given the prevalent use of
Cartesian coordinates, the temptation may be great to think of each vector as a
triplet of numbers with respect to some background Cartesian basis , , . However, this would obscure the primary
decompositional role of the covariant basis. The covariant basis is
used for decomposing other vectors but itself need not be decomposed. The buck, so to say, stops
with .
9.2.3Visualizing the covariant basis
The primary geometric characteristic of the vectors is
that they are tangential to the corresponding coordinate lines.  (9.13) To see
why this is so for, say,textbf{ },
consider the function
(9.13) To see
why this is so for, say,textbf{ },
consider the function
 (9.13)
(9.13) (Note that we are now using the
letter to denote yet another function, this time of one variable
.) The vectors trace out the coordinate line corresponding
to .
Therefore, as we studied in Chapter 5, the
derivative
is tangential to that coordinate
line. Of course, since is the same as
we conclude that the vector is
tangential to the coordinate line corresponding to , as
we set out to show.
The covariant basis is particularly easy to visualize when the coordinate lines are drawn at
integer increments, as in the following two-dimensional figure.  (9.17) In
the context of such a representation, the approximate length of at a
node is such that its tip is located in the vicinity of the neighboring node whose
coordinate
exceeds that of its tail by . For example, the tip of the vector at the
point with coordinates falls near the point with coordinates . This is so because, in the limit
(9.17) In
the context of such a representation, the approximate length of at a
node is such that its tip is located in the vicinity of the neighboring node whose
coordinate
exceeds that of its tail by . For example, the tip of the vector at the
point with coordinates falls near the point with coordinates . This is so because, in the limit
 (9.17)
(9.17) the "intermediate" vector
corresponding to the finite value falls exactly at the point with coordinates and, in the limit as approaches , it ought to be approximately so.
9.2.4The covariant basis in various coordinate systems
9.2.5In affine coordinates
For general curvilinear coordinate systems, the covariant basis varies from one point to
another. In an affine coordinate system, thanks to its regularity, the covariant basis is
the same at all points and coincides with the coordinate basis , , . 
 (9.19) In other words, the basis vector points
from the point with coordinates to the point whose -th coordinate is increased by . For example, points
from the point with coordinates to the point with coordinates . In curvilinear coordinates, the
preceding statement is approximately true at points where the magnitude of the second
derivatives of is not too great.
(9.19) In other words, the basis vector points
from the point with coordinates to the point whose -th coordinate is increased by . For example, points
from the point with coordinates to the point with coordinates . In curvilinear coordinates, the
preceding statement is approximately true at points where the magnitude of the second
derivatives of is not too great.

 (9.19)
(9.19) Since Cartesian coordinates are a special case of affine coordinates, the Cartesian covariant
basis is the same at all points. Cartesian coordinate lines form a regular orthogonal unit grid and
therefore the covariant basis consists of orthogonal unit, i.e. orthonormal, vectors. The following
figure shows the Cartesian covariant bases in two and three dimensions. 
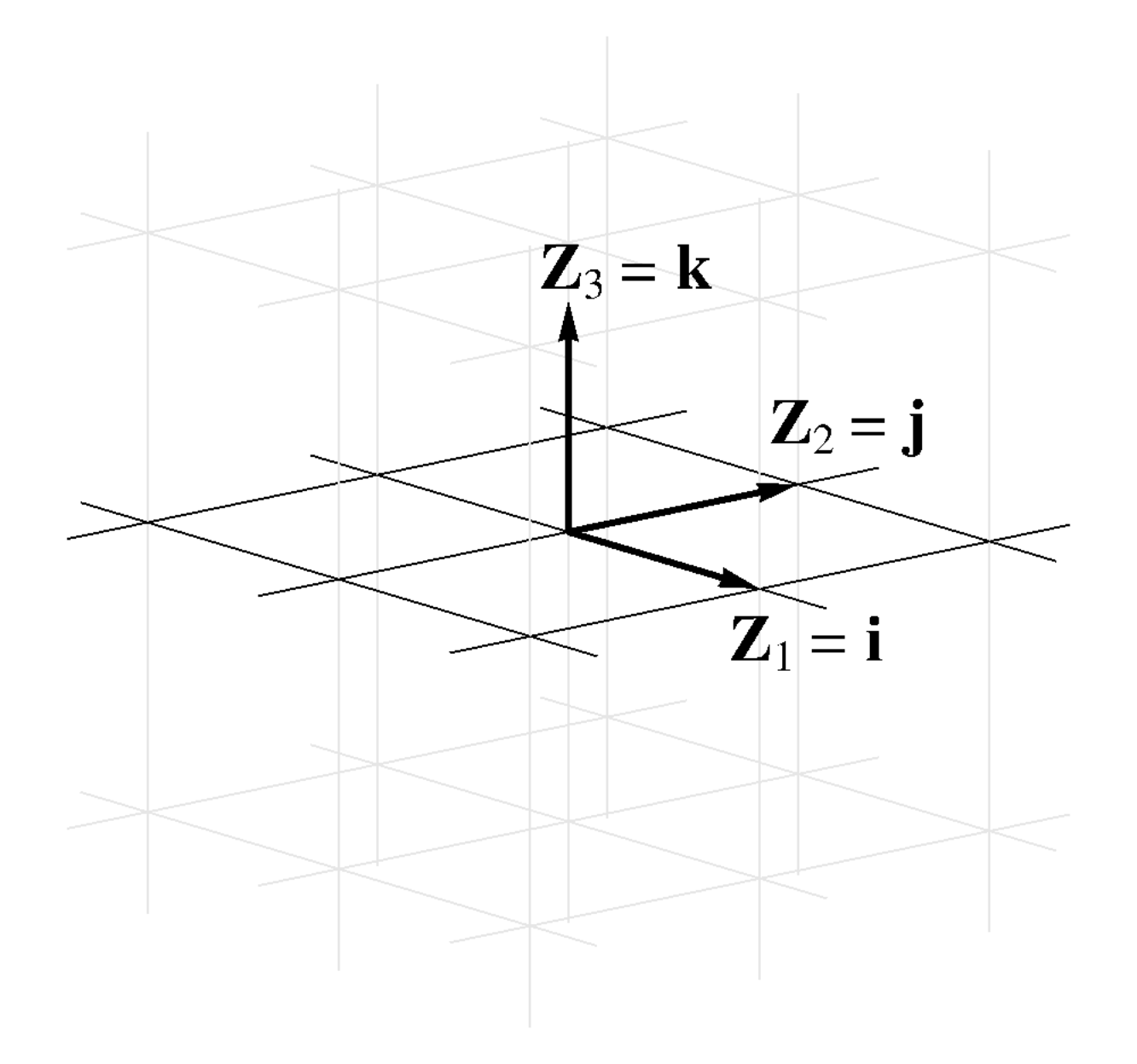 (9.20) In conclusion, the familiar affine basis , , fits perfectly into the new framework where the coordinate
basis is constructed by differentiating the position vector with respect to each of the coordinates.
(9.20) In conclusion, the familiar affine basis , , fits perfectly into the new framework where the coordinate
basis is constructed by differentiating the position vector with respect to each of the coordinates.

 (9.20)
(9.20)9.2.6In polar coordinates
In polar coordinates , the coordinate
corresponds to and
corresponds to . The covariant basis vector , given
by the equation  (4.24) Of
course, this configuration corresponds exactly to the calculation of . Thus,
is a
vector of length that points in the counterclockwise
tangential direction to the coordinate circle. These findings regarding the covariant basis for
polar coordinates are illustrated in the following figure.
(4.24) Of
course, this configuration corresponds exactly to the calculation of . Thus,
is a
vector of length that points in the counterclockwise
tangential direction to the coordinate circle. These findings regarding the covariant basis for
polar coordinates are illustrated in the following figure.  (9.23)
(9.23)
is a unit vector that points
in the radial direction away from the origin . Demonstrating this fact is left as
an exercise. The vector is
given by
Recall from Section 4.3 that the derivative of the position vector tracing out a circle of radius is a vector tangential to the circle
also of length .
 (4.24)
(4.24) (9.23)
(9.23)Observe that the covariant basis in polar coordinates is orthogonal. Interestingly, in some
textbooks, the vector is
scaled to unit length in order to produce an orthonormal basis at every point. This is
highly inadvisable due to the numerous disadvantages in exchange for little gain.
Polar coordinates present us with our first example of a coordinate basis that varies from one
point to another. This variability is of enormous importance. Some of its most crucial implications
are described below in Section 9.2.10 and will be
discussed further later in our narrative.
9.2.7In cylindrical coordinates
Cylindrical coordinates augment polar coordinates with the coordinate whose coordinate lines are straight
lines orthogonal to the coordinate plane. Within each plane parallel to the coordinate plane, i.e.
within each coordinate surface corresponding to a constant , the vectors  (9.26)
Note that even with the addition of , the
covariant basis remains orthogonal.
(9.26)
Note that even with the addition of , the
covariant basis remains orthogonal.
coincide with the covariant basis in
polar coordinates. The additional vector , given
by
is a constant unit vector orthogonal
to the coordinate plane that points in the "upward" direction -- in other words, the set , , is
positively oriented.
 (9.26)
(9.26)9.2.8In spherical coordinates
In order to describe the covariant basis in
spherical coordinates , we will use a combination of words and figures. The
first vector  (9.30) As
was the case with cylindrical coordinates, the basis is
positively oriented. Furthermore, it is orthogonal but not orthonormal.
(9.30) As
was the case with cylindrical coordinates, the basis is
positively oriented. Furthermore, it is orthogonal but not orthonormal.
is a unit vector that points in the
radial direction away from the origin . The second vector
corresponds to the rate of change in
the position vector along a meridian. Thus, is a
vector of length that points in the direction
tangential to the meridian away from the north pole, i.e. the point with . The third vector
corresponds to the rate of change in
the position vector along a parallel and is thus tangential to that
parallel. Since a parallel at colatitude has radius , the length of is
also . The following figure shows the basis
vectors and
on the
coordinate sphere of radius .
 (9.30)
(9.30)9.2.9Orthogonal coordinate systems
As we have pointed out, the covariant bases for Cartesian, polar, cylindrical, and spherical
coordinates are orthogonal. Coordinate systems that have this property are themselves known
as orthogonal. Since the covariant basis vectors are tangential to the coordinate lines,
orthogonal systems can be equivalently characterized by orthogonal coordinate lines. There is no
particular significance to orthogonal coordinate systems, except that some calculations are
simplified. The following figure shows the coordinate lines for a generic orthogonal system.  (9.31)
(9.31)
 (9.31)
(9.31)You may be wondering whether there exist orthonormal coordinate systems other than
Cartesian. The surprising answer is no: as we discuss below in Section 9.3.6, all orthonormal coordinates are necessarily
Cartesian.
9.2.10On the spatial variability of the covariant basis
If you are coming from an exclusively affine background, the implications of the spatial
variability of the covariant basis in curvilinear coordinates may require some getting used to. In
some ways, the difference is dramatic. For example, the components of one and the same vector
calculated at different points are likely to be distinct. Conversely, two vectors with identical
components are likely to be distinct. Furthermore, vectors at different points cannot be added
together by adding their components. This insight has a number implications, including for
integration which, in essence, is a form of addition. Suppose that represent the components of the gravitational
force field per unit mass acting upon a body with density that occupies the domain . If the coordinate system as affine, then the components
of
the total force are given by the integral
In curvilinear coordinates, on the
other hand, the above integral is meaningless since it requires the addition of components of
vectors calculated with respect to (an infinity of) different bases.
These difficulties, however, should not in any way dissuade us from utilizing curvilinear
coordinates whose use is essential in most situations. Furthermore, in many geometric spaces, such
as the surface of a sphere and most other curved surfaces, curvilinear coordinates are the
only available option. And even when affine coordinates are feasible, curvilinear
coordinates may nevertheless be a natural choice and experience shows that overcoming
difficulties that stem from natural choices is always a worthwhile endeavor. Indeed, our future
experience will demonstrate that allowing curvilinear coordinates is an unequivocal improvement
over the exclusive use of affine coordinates. The additional complexity will prove to be not an
obstacle but an impetus for deeper insights that would not have been come form affine analysis.
9.3The covariant metric tensor
9.3.1The definition
We have arrived at one of the central objects in our subject: the covariant metric tensor. By
definition, the elements of the covariant metric tensor
are the pairwise dot products of the covariant basis vectors , i.e.
Since the dot product is
commutative, the metric tensor is symmetric, i.e.
and can be organized into a
symmetric matrix
This matrix is entirely analogous to
the dot product matrix
from Chapter 2.
The central role of the covariant metric tensor is to facilitate the calculation of dot products --
and thus of lengths and angles -- in the coordinate space. In the next Chapter, we will show that
the dot product of vectors with components and
is
given by
Thus, the term metric refers
to covariant metric tensor's role in representing geometric measurements.
A few sections below, we will introduce the contravariant metric tensor
as the matrix inverse of the covariant metric tensor .
Because it will almost always be clear from the context which of the two objects we are referring
to, the adjectives covariant and contravariant are often dropped and the shorter term
metric tensor is used to describe both tensors. The terms fundamental tensor and
fundamental form can also be used to describe both metric tensors.
When we write the covariant basis directly in terms of the position vector , i.e.
we see the entire scope of its
construction from the position vector which we chose as the starting point of our analysis. The
recipe requires the ability to measure distances and angles (which go into the dot product), as
well as the ability to differentiate vector-valued functions with respect to the coordinates.
However, once the metric tensor is
calculated, it can be used to calculate the dot product, and therefore distances and angles, in the
component space by analytical means. Furthermore, as we will soon discover, the metric tensor plays
a crucial role in the component space differentiation of vector-valued functions, again by
analytical means. These abservations suggest the possibility of an entirely new approach to the
subject of Geometry where the metric tensor -- rather than lengths and angles -- serves as
the starting point. The fundamentals of this approach, known as Riemannian Geometry, will be
outlined in Chapter 20.
9.3.2In affine and Cartesian coordinates
In affine coordinates, the covariant basis is the
same at all points and, therefore, so is the metric tensor .
Using the symbols , , and to denote the elements of the covariant basis, the metric
tensor
correspond to the constant matrix
For a specific two-dimensional example, consider the affine coordinate system illustrated in the
following figure, where the length of is , the length of is , and the angle between and is .  (9.38) Then
(9.38) Then
 (9.38)
(9.38) In Cartesian coordinates, the covariant basis is orthonormal and, therefore,
corresponds to the identity matrix
Generally speaking, in an -dimensional Euclidean space, the elements of the
Cartesian metric tensor can be captured by the equation
Note that we are careful not
to use the Kronecker delta symbol on
the right since its indicial signature does not match that of
and therefore the equation
would have been invalid from the tensor notation point of view. That said, once we introduce
index juggling in Chapter 11, we will
establish a surprising equivalence between the metric tensor and the Kronecker delta symbol.
9.3.3In polar coordinates
Recall that the covariant basis in polar coordinates consists of two orthogonal vectors and
of
lengths and . Therefore, the covariant metric
tensor
has two nonzero elements
Thus,
The diagonal property of the resulting matrix reflects the orthogonality of the coordinate system.
It is interesting to note that the elements of
have varying "units" of length. If meter is used as the unit of length in the Euclidean
space, then is
dimensionless while is
measured in square meters. The units of the off-diagonal zero entries are meters.
While the issue of units is quite subtle, we will be able to side step it completely throughout our
narrative.
9.3.4In cylindrical coordinates
Since the cylindrical covariant basis consists of orthogonal vectors , and
of
lengths , , and ,
9.3.5In spherical coordinates
Based on the above description of the covariant basis in
spherical coordinates, it is an entirely straightforward matter to show that in spherical
coordinates,
9.3.6Restoring the coordinate system from the metric tensor
Two different coordinate systems related by a rigid transformation, i.e. a combination of rotation,
reflection, and translation, produce the same covariant metric tensor function . For example, the following figure shows a
rotation of a coordinate system by an angle followed by translation by a vector
.  (9.46) It is clear that is unchanged under this transformation since
the relative arrangement of the covariant basis vectors is exactly the same at corresponding
points.
(9.46) It is clear that is unchanged under this transformation since
the relative arrangement of the covariant basis vectors is exactly the same at corresponding
points.
 (9.46)
(9.46)Interestingly, the converse is also true: if two coordinate systems are characterized by the same
covariant basis function then they are necessarily related by a rigid
transformation. This statement is the object of Problem 9.1 at the end of this Chapter. This
observation shows that the covariant metric tensor
retains a great deal of information about the coordinate system. In fact, it retains all the
information, except its absolute location and orientation (in the sense of rotation and
reflection).
In particular, if the elements of the metric tensor
form the identity matrix, then the coordinate system is necessarily Cartesian. In other words, all
orthonormal coordinates are Cartesian. In other words, there cannot exist a coordinate
system, such as the one "illustrated" in the following figure, where the covariant basis is
orthonormal at every point, while the coordinate lines are not straight.  (9.47)
(9.47)
 (9.47)
(9.47)9.4The volume element
9.4.1The definition
Denote by the determinant of the matrix
corresponding to covariant metric tensor ,
i.e.
According to our discussion in
Chapter 3, equals the square of the
volume of the parallelepiped formed by the vectors , , and
.
Therefore, its square root
equals the conventional (unsigned) volume of the same parallelepiped. As a result,
is known as the volume element. In a two-dimensional space,
may be referred to as the area element while in a one-dimensional space, it may be referred
to as the line element. When the dimension of the space is not specified, the term volume
element is preferred.
You will recall that the symbol is also used to denote the coordinate
arguments of a function in compressed fashion, as in the symbol which represents the function . Of course, whether is used in the sense of the
determinant of or
the coordinates as
the arguments of a function is always clear from the context. In fact, since the determinant of
can be treated as a function of the coordinates , the
two symbols can be combined into a single expression that represents the function , i.e. the determinant of as
a function of the coordinates. In Chapter 16, we
will consider the derivative of
this function.
9.4.2The role of in integration
The volume element
plays an important role in many aspects of Tensor Calculus. Due to the fact that it equals volume
of the parallelepiped formed by the elements of the covariant basis, it is not surprising that it
is featured prominently in integration. While the topic of integration will be discussed thoroughly
in a future book, the purpose of this Section is to illustrate, on an intuitive level, why
appears as a factor in the coordinate representation of integrals.
Suppose that a two-dimensional domain is referred to a curvilinear coordinate system .
Consider the covariant basis at a
point with coordinates .  (9.50)
It is apparent that the area of the parallelogram formed by and
is
approximately equal to the coordinate parallelogram formed by the curved segments of
the coordinate lines connecting the points with coordinates , , , and . Of course, the difference between the
two areas is relatively significant since is a relatively large increment. For a smaller increment
, the difference between the scaled value and
the area of the coordinate parallelogram with vertices at the points , , , and is smaller. The following figure shows the
coordinate parallelogram for as well as the parallelogram formed by and . It is apparent that the discrepancy between the two
areas is dramatically smaller.
(9.50)
It is apparent that the area of the parallelogram formed by and
is
approximately equal to the coordinate parallelogram formed by the curved segments of
the coordinate lines connecting the points with coordinates , , , and . Of course, the difference between the
two areas is relatively significant since is a relatively large increment. For a smaller increment
, the difference between the scaled value and
the area of the coordinate parallelogram with vertices at the points , , , and is smaller. The following figure shows the
coordinate parallelogram for as well as the parallelogram formed by and . It is apparent that the discrepancy between the two
areas is dramatically smaller.  (9.51) As the increment approaches zero, the discrepancy between the areas
approaches zero faster than and
therefore the sum of the growing number of terms
approaches the area of the domain, i.e.
(9.51) As the increment approaches zero, the discrepancy between the areas
approaches zero faster than and
therefore the sum of the growing number of terms
approaches the area of the domain, i.e.
 (9.50)
(9.50) (9.51)
(9.51) Meanwhile, the sum
approaches the repeated integral
where the limits of integration on
the right are chosen as to describe the region . Thus,
Similarly, the geometric integral
for a field can be converted to the repeated
integral
We will refer to the repeated
integrals on the right as arithmetic integrals since they are divorced from the geometric
problem from which they arose and can be evaluated by the techniques of Calculus or by a
computational method.
Our experience with geometric integrals such as reflects our broader experience with geometric objects.
That is, while they provide us with great geometric insight, they do not give us the ability to
make any specific calculations for specific problems. In order to perform a specific calculation,
we must convert the geometric integral to an arithmetic integral which requires the use of the
volume element .
The foregoing discussion was our first example of translating a geometric analysis into the
coordinate space.
9.4.3The volume element in various coordinates
In affine coordinates, the volume element is a constant given by the equation
A more specific expression can be
given only if further details about the coordinate system are available. For the two-dimensional
affine coordinates considered earlier, we have
In Cartesian coordinates, the
volume element has a constant value of , i.e.
In polar coordinates, we have
In cylindrical coordinates, we
similarly have
Finally, in spherical coordinates, we have
As a demonstration of the utility of
in integration, let us calculate the area of a circle of radius in polar coordinates. We have
In other words,
which is easily evaluate to produce
Similarly, the volume of a sphere of radius is given by
These are classical examples of the
advantage of using the appropriate coordinate system for every problem.
9.5The contravariant metric tensor
9.5.1The definition
The contravariant metric tensor
is defined as the "matrix inverse" of the covariant metric tensor ,
i.e.
Since the inverse of a symmetric positive definite matrix is itself symmetric and positive
definite, the contravariant metric tensor also has this important property.
The definition of the contravariant metric tensor can be captured in the tensor notation, albeit
implicitly, by the equation
Thus, the tensor notation strongly
suggests the use of superscripts for the new object and the corresponding use of the term
contravariant. As usual, this placement will prove to be the correct predictor of the manner
in which this object transforms under coordinate transformations.
A well-known fact from Linear Algebra tells us that a matrix commutes with its inverse. Therefore,
the contraction ,
which we can also write as ,
yields the Kronecker delta symbol, as well, i.e.
Of course, in the case of the metric
tensors, this relationship also follows from their symmetric property. However the argument based
on the commutativity of a matrix with its inverse is more general.
Looking ahead, the contravariant metric tensor will provide our framework with much needed
"contravariance" and thus help balance the numbers of superscripts and subscripts. As we discussed
in Chapter 14, such balance is essential to
achieving invariance.
9.5.2The operation of inverting the metric tensor
Suppose that the system is
obtained from by
contraction with the contravariant metric tensor ,
i.e.
From this relationship, it can be
shown -- thanks to the matrix inverse relationship between the two metric tensors -- that
can be obtained from by
contraction with the covariant metric tensor, i.e.
Of course, the connection between
the above two identities is analogous to that between the Linear Algebra identities
and
where is an invertible matrix, while and are, typically, matrices or, more generally, matrices.
In elementary algebra, we show that follows from by dividing both sides of by . In Linear Algebra, the analogous tactic is stated in
terms of multiplication by .
Multiplying both sides of
by , we
have
Since and , we find that
or
as we set out to show.
Let us now use the tensor notation to apply the same logic to the identity
Contracting both sides with , we
have
Since
and , we
find
or
Renaming into , we arrive at the desired identity
In summary,
By analogy with Linear Algebra, we
will refer to the tactic that converts the former identity into the latter as inverting the
metric tensor. Note that inverting the metric tensor works just as well in the reverse
direction, i.e.
Furthermore, it also works for
systems with indicial signatures of arbitrary complexity. For example,
9.5.3The contravariant metric tensor in various coordinate systems
In a general affine coordinate system,
In particular, for the specific affine coordinates considered above, where
we find, by inverting this matrix, that
In Cartesian coordinates, where the covariant metric tensor
corresponds to the identity matrix, so does the contravariant metric tensor ,
i.e.
In polar coordinates,
In cylindrical coordinates,
In spherical coordinates,
As a preview of the important role of the contravariant metric tensor, consider the formula
for the Laplacian of a
function in spherical
coordinates (derived in Chapter 18), where you can
see, especially in the last two terms, the distinctive influence of the contravariant metric
tensor.
9.5.4The vital role of the contravariant metric tensor
The role of the contravariant metric tensor in Tensor Calculus is indeed indispensable. As an
object with superscripts, it provides the necessary counterbalance for the objects with
subscripts, of which there is no shortage since differentiation naturally leads to objects
with subscripts. Once again, the significance of such a balance is straightforward:
invariants -- the ultimate objects of our investigations -- are formed by contracting away
all indices, which naturally requires a balance of superscripts and subscripts.
Another insight into the importance of the contravariant metric tensor comes from Section 2.4 where we discussed linear decomposition by means of the
dot product. Operating without superscripts, we showed that the components , , and
of a
vector with respect to a basis , not
necessarily orthogonal, are given by the equation
Since the matrix that is being
inverted corresponds to the covariant metric tensor ,
the inverse corresponds to the contravariant metric tensor .
Thus, we can anticipate that the contravariant metric tensor plays a central role in the
determination of the components of a vector. This is, indeed, the case as we will shortly discover
in Chapter 10.
9.6The contravariant basis
9.6.1The definition
The contravariant basis is
obtained by contracting the covariant basis
and the contravariant metric tensor ,
i.e.
Since
is symmetric, it makes no difference whether the first or the second index is used in the
contraction. In Chapter 11, we will learn that the
contraction on the right is an example of index juggling.
By inverting the metric tensor, as described in Section 9.5.2, we note the inverse relationship
In other words, the covariant basis
can be
obtained by contracting the contravariant basis with the covariant metric tensor. Thus, we are able
to easily move back and forth between the covariant and contravariant bases by contraction with the
appropriate metric tensor.
9.6.2The identity
Recall that, by definition, the pairwise dot products of the covariant basis vectors
produce the elements of the covariant metric tensor ,
i.e.
Similarly, the pairwise dot products
of the elements of contravariant basis
produce the contravariant metric tensor ,
i.e.
This relationship is demonstrated by
the chain of identities
Justifying each step in the above
derivation is left as an exercise.
When viewed side by side, the relationships
and
show the close parallel between the covariant and contravariant types of objects, which will become
more general with the introduction of index juggling in Chapter 11.
9.6.3The identity
Finally, we will now demonstrate the identity
which shows that the contravariant
and covariant bases are mutually orthonormal. In other words, each element of the
contravariant basis is orthogonal to every differently-numbered element of the covariant
basis and vice versa. Additionally, the dot product of each element of one basis with the
same-numbered element of the other basis is . This relationship can also be proved by the simple
chain of identities
As we concluded in the very last sentence of Section 2.4,
a vector is uniquely determined by its dot products with the elements of a basis. Thus, the
identity
can actually be taken as the
definition of the contravariant basis as it
specifies the values of the dot products of each vector with
every element of the covariant basis .
Indeed, the equation
gives us an actionable
geometric recipe for constructing the contravariant basis. For example, in order to
construct note
that it is orthogonal to and
which
uniquely determines the straight line containing . The
fact that the dot product is
, which is positive, implies that lies
in the same half-space as --
otherwise the angle between and
would
be greater than resulting
in a negative dot product. Therefore, the only remaining unknown is the length of which
is easily determined from the equation
i.e.
where is the already-determined angle
between and
. Thus,
which completes the construction of
.
The reader may want to think through the two-dimensional case on their own. The figure below shows
a covariant basis and
the corresponding contravariant basis from
the example that follows.  (9.98)
(9.98)
 (9.98)
(9.98)9.6.4In various coordinate systems
In affine coordinates, the contravariant basis is given by the matrix identity  (9.103) As
an exercise, confirm by evaluating dot products, that is
orthogonal to and is
orthogonal to .
(9.103) As
an exercise, confirm by evaluating dot products, that is
orthogonal to and is
orthogonal to .
and nothing more specific can be
said in general. For the two-dimensional example considered previously, we have
i.e.
The resulting vectors and
are
illustrated in the following figure.
 (9.103)
(9.103)In Cartesian coordinates, since the contravariant metric tensor corresponds to the identity matrix,
the contravariant and the covariant bases are the same, i.e.
Recall that, in polar coordinates,  (9.110)
(9.110)
Thus,
i.e.
In words, the vector
coincides with , while
points in the same direction as and
has length . The following figure
illustrates the contravariant basis in polar coordinates.
 (9.110)
(9.110) It is left as an exercise to show that in cylindrical coordinates,
Likewise, it is left as an exercise to show that in spherical coordinates,
9.7The orientation of a coordinate system
In Section 3.1, we introduced the concept of
orientation for a complete set of linearly independent vectors. This concept can be applied
to the covariant basis and in
this way extended to coordinate systems. Namely, the orientation of a coordinate system is
identified with the orientation of the covariant basis: a coordinate system is said to be
positively oriented or right-handed if the covariant basis is positively oriented,
and negatively oriented or left-handed otherwise.
Naturally, the orientation of the coordinate system depends on the order of the coordinates. When
the indicial notation is used to denote the coordinates , the
order is obvious. However, when special letters are used for special coordinates (such as , , ), the order must be explicitly specified. In all special
coordinate systems introduced in this book, the order of the variables was chosen so that the
coordinate system is positively oriented.
Generally speaking, the orientation is a local property defined at a point and may change from one
region to another. When this occurs, the covariant "basis" vectors fail to be linearly independent
on the boundary between the two regions. This signals a singularity that requires special care.
Finally, recall that two sets of vectors have the same orientation if they are related by a matrix
with a positive determinant. Since the covariant and the contravariant bases are related by the
metric tensor ,
which is positive definite matrix and therefore has a positive determinant, the two bases have the
same orientation. Thus, we may refer to the orientation of the coordinate basis, without indicating
its flavor.
9.8Exercises
Exercise 9.1Show that in affine coordinates, the basis vector connects the point with coordinates with the point whose -th coordinate is increased by .
Exercise 9.2Show that in polar coordinates, the basis vector
is a unit vector that points in the outward radial direction. Similarly, show that
in spherical coordinates is a unit vector that points in the outward radial direction.
Exercise 9.3Show that (the matrix corresponding to) the covariant metric tensor is positive definite. In fact, any matrix consisting of pairwise dot products of linearly independent vectors is positive definite.
Exercise 9.4Consider the identity
and contract both sides with , i.e.
or,
Using this identity, demonstrate that the contravariant metric tensor is symmetric.
Exercise 9.5For the angle between and , show that
and therefore
Note that the numerator in the fraction above corresponds to the determinant of the submatix
of the covariant metric tensor.
Exercise 9.6Show that in the -dimensional space,
Exercise 9.7Show that inverting the metric tensor also works in the direction opposite of that described in Section 9.5.2, i.e.
implies
Exercise 9.8Show that inverting the metric tensor works for systems with indicial signatures of arbitrary complexity, e.g.
implies
Exercise 9.9Justify each step in the following chain of identities:
Exercise 9.10Justify each step in the following chain of identities:
Exercise 9.11Show that the angle between and is less than and that the product of the lengths of the two vectors is at least .
Exercise 9.12What are the components of with respect to the covariant basis and what are the components of with respect to the contravariant basis ?
Problem 9.1Devise an algorithm for restoring the coordinate system from the metric tensor . As we discussed in Section 9.3.6, this can be done only to within a rigid transformation. Refer to Problem 2.3 as a suggestion for the first step in the algorithm.