Vector Calculus extends the ideas of Calculus to vector fields. As such, one would expect Vector Calculus to be full of remarkable connections and elegant identities. This is, in fact, so -- but only when the right language is chosen for the description. Surprisingly, the language of geometric vectors, which has served us so well in our initial explorations, proves to be ill-equipped at dealing with even some of the most elementary combinations involving vector fields and their derivatives..

To illustrate this point, consider the dot product $\mathbf{U}\cdot\mathbf{V}$ of two vector fields $\mathbf{U}$ and $\mathbf{V}$. Since $\mathbf{U} \cdot\mathbf{V}$ is a scalar field, it is subject to the gradient operator $\mathbf{\nabla}$. As a matter of fact, the combination $\mathbf{\nabla }\left( \mathbf{U}\cdot\mathbf{V}\right)$ is commonly found in numerous applications. And since the gradient satisfies the product rule for scalar fields, we expect to find a similar rule for the dot product of vector fields, i.e. However, this identity is nonsensical as there is no such thing as $\mathbf{\nabla U}$ since the gradient cannot be applied to a vector field. Thus, we have failed in one of the most elementary endeavors of Vector Calculus.

To understand the root cause of the problem, let us borrow one of our own paragraphs from Chapter 2 in which we addressed the effectiveness of the language of geometric vectors: As we will quickly discover, working with geometric quantities leads to greater organization of thought. Geometric vectors have fewer algebraic capabilities compared to numbers. This is a positive: the small number of accessible operations focuses our attention on the few that are available. However, when it comes to more sophisticated analyses, what has been a positive will now become a negative. Geometric vectors are simply not rich enough algebraically to accommodate the more advanced demands of Vector Calculus.

There are two possible ways out. The first way, and one that is central to our narrative, is to introduce coordinates in order to switch from vectors to their components. In a microcosm, the immense utility of this approach can be illustrated by the aforementioned gradient of a dot product In terms of components, the dot product $\mathbf{U}\cdot\mathbf{V}$ is $U_{i}V^{i}$ and the components of the gradient are given by Next, an effortless application of the product rule for the covariant derivative yields Naturally, the gradienttextbf{ }$\mathbf{\nabla}\left( \mathbf{U} \cdot\mathbf{V}\right)$ itself is produced by contracting $\nabla_{k}\left( U_{i}V^{i}\right)$ with $\mathbf{Z}^{k}$, i.e. and the calculation is complete.

Note, however, that the restoration of the geometric invariant $\mathbf{\nabla }\left( \mathbf{U}\cdot\mathbf{V}\right)$ need not take place at this point if further analysis is to be conducted. And, although the combinations $\nabla_{k}U_{i}~V^{i}$ and $U_{i}~\nabla_{k}V^{i}$ are devoid of direct geometric interpretation, they can be easily subjected to further analysis. Meanwhile, the geometric meaningfulness of the eventual results is assured by the tensor framework.

In summary, the identity has all the simplicity and the structure of its meaningless counterpart and at the same time enables us to take full advantage of the tensor framework.

The alternative approach, known as dyadic, doubles down on the geometric aspect of vectors in order to avoid the use of coordinate systems at all costs. In the dyadic approach, all objects are assigned some invariant meaning characterized by their interactions with other objects. For example, the object $\mathbf{\nabla U}$ would be described as a linear transformation that can be applied to any other vector $\mathbf{V}$ with the result denoted by $\mathbf{\nabla U}\left( \mathbf{V}\right)$, $\left( \mathbf{\nabla U},\mathbf{V}\right)$, or simply by $\mathbf{\nabla U}\cdot\mathbf{V}$. No doubt, this operation would be defined in such a way that it produces, without mentioning it explicitly, the vector $\mathbf{Z}^{k}V^{i}\nabla_{k}U_{i}$, thus achieving the same result, but axiomatically and without a reference to the components of vectors.

This simple example illustrates the unfortunate side effect of the dyadic approach: the need for new kinds of objects and new kinds of operators. The resulting framework never reaches algebraic closure, i.e. a framework with a finite number of kinds of objects and operators where the result of applying an existing kind of operator to an existing kind of object always produces an object of an existing kind. A visit to the Vector calculus identities page on Wikipedia reveals identities such as where each identity clearly attempts to capture the elementary product rule, but is only able to do so by relying on novel kinds of objects and operators. This experience is perfectly captured by Hermann Weyl's quote from his classic Space Time Matter: In trying to avoid continual reference to the components we are obliged to adopt an endless profusion of names and symbols, in addition to an intricate set of rules for carrying out calculations, so that the balance of advantage is considerably on the negative side. An emphatic protest must be entered against these orgies of formalism which are threatening the peace of even the technical scientist.

Let us, then, set the dyadic approach aside and concentrate on the coordinate approach supported by the techniques of Tensor Calculus. In this Chapter, we will discuss four classical differential operators: the gradient, the divergence, the Laplacian, and the curl. Of course, each one of these operators is some combination involving the covariant derivative. This highlights one of the strengths of Tensor Calculus: its highly restricted set of underlying operations. In a Euclidean space, all objects and operations are expressed in terms of addition, multiplication, contraction, and the higher-level construct of the covariant derivative.

When a coordinate system $Z^{i}$ is imposed upon a Euclidean space, we are automatically provided with a number of tensors that can be used in various combinations, including the covariant and the contravariant bases $\mathbf{Z}_{i}$ and $\mathbf{Z}^{i}$, the metric tensors $Z_{ij}$ and $Z^{ij}$, and the Levi-Civita symbols $\varepsilon_{ijk}$ and $\varepsilon ^{ijk}$. These basic elements, along with the covariant derivative $\nabla _{i}$ will act as jigsaw puzzle pieces in the construction of the invariant differential operators. Interestingly, the metric tensor will rarely appear explicitly in our expressions since, thanks to index juggling, it gets absorbed into the tensor with which it is contracted. Nevertheless, its continual presence is revealed in the placement of indices.

For a scalar field $U$, one way to form a differential invariant is to contract $\nabla_{i}U$ with $\mathbf{Z}^{i}$, resulting in the vector We instantly recognize this combination as the gradient $\mathbf{\nabla}U$ of $U$, which can also denoted by the symbol $\operatorname{grad}U$, i.e.

Note that a similar combination cannot be formed for a vector field $\mathbf{U}$ since the product $\mathbf{Z}^{i}\nabla_{i}\mathbf{U~}$is meaningless. This reminds of the fact that we mentioned in Chapter 4 that there is no such thing as the gradient of a vector field. That said, the dot product $\mathbf{Z}^{i}$ and $\nabla_{i}\mathbf{U}$, which is discussed below, is quite meaningful.

Another meaningful invariant combination involving a scalar field $U$ is $\nabla_{i}\nabla^{i}U$. This operation is known as the Laplacian of $U$ and can be denoted by $\Delta U$, i.e. Unlike the gradient, the Laplacian can be applied to vector fields. Indeed, the combination represents is a perfectly well-defined tensor expression. For instance, the Laplacian can be applied to the position vector $\mathbf{R}$ and it is left as an exercise to show that the result is zero. Since the Laplacian of an invariant is itself an invariant, it immediately raises the question of its geometric interpretation. While some invariants do not have a simple geometric interpretation, the Laplacian does, and it will be described later in this Chapter.

Among combinations that can be applied to first-order tensors $U^{i}$, the most natural one is, undoubtedly, known as the divergence of the tensor field $U^{i}$. Note that the Laplacian of a scalar $U$ (unrelated to $U^{i}$ in the previous sentence) is equivalent to the divergence of the tensor $\nabla^{i}U$.

The divergence $\nabla_{i}U^{i}$ can also be thought of as being associated with the vector field $\mathbf{U}=U^{i}\mathbf{Z}_{i}$. Thus, the combination $\nabla_{i}U^{i}$ can be referred to as the divergence of the vector field $\mathbf{U}$ and, in that context, be denoted by $\mathbf{\nabla} \cdot\mathbf{U}$ or $\operatorname{div}\mathbf{U}$, i.e. textbf{ }It is left as a simple exercise to that $\operatorname{div} \mathbf{U}$ is given by the equation

The logic that has led us to the gradient, the Laplacian, and the divergence illustrates that the tensor framework not only provides us with a framework for analyzing the invariant properties of a given object, but also gives us clear and exhaustive instructions for constructing new invariants. For example, observe that an invariant combination must have an even number of indices and, therefore, $2$ is the least nonzero number of indices that an invariant can have. Thus, from this "orchestration" point of view, it is a trivial observation -- and yet it is a profound insight -- that the gradient, the Laplacian, and the divergence are the only possible invariant expressions involving the symbols $\nabla_{i}$, $U$, $\mathbf{U}$, $U^{i}$, and $\mathbf{Z}^{i}$ -- with the implied possibility of index juggling. Of course, since the Laplacian is the divergence of gradient, we could reduce the number of elementary differential operators to two, but it is worthwhile to treat the Laplacian as an equal partner.

More complicated invariant expressions with an even number of indices, such as $\nabla_{i}\nabla_{j}\nabla^{i}U~\mathbf{Z}^{j}$, $\nabla_{j}\nabla^{j} \nabla_{i}\nabla^{i}U$, and $\nabla^{i}\nabla_{j}\nabla_{i}U^{j}$, can always be viewed as combinations of the gradient, the Laplacian, and the divergence. For example, the combination $\nabla_{i}\nabla_{j}\nabla^{i}U~\mathbf{Z}^{j}$ is the Laplacian of the gradient of $U$, which becomes apparent when the expression is rewritten as with parentheses added strictly for stylistic purposes. Meanwhile, $\nabla _{j}\nabla^{j}\nabla_{i}\nabla^{i}U$ is the Laplacian of the Laplacian of $U$. This combination is known as the biharmonic operator and plays an important role in the theory elasticity. Finally, $\nabla^{i}\nabla_{j} \nabla_{i}U^{j}$ when rewritten as is easily identified as the Laplacian of the divergence of $U^{j}$.

Of course, with the introduction of additional objects, further invariant operators can be formed. For example, with the help of the Levi-Civita symbol $\varepsilon^{ij}$ in two dimensions, we can form the combination $\varepsilon^{ij}\nabla_{i}U_{j}$ which is the two-dimensional version of the classical curl. In three dimensions, the combination $\varepsilon ^{ijk}\nabla_{i}\nabla_{j}$ leaves a free index that can be contracted with $\mathbf{Z}_{k}$ to form the combination $\varepsilon^{ijk}\nabla_{i} \nabla_{j}\mathbf{Z}_{k}$, which is the actual curl. We will discuss the curl, both in two and three dimensions, later in the Chapter. Meanwhile, we will turn our attention to the geometric interpretations the Laplacian and divergence, having described the geometric interpretation of the gradient in Chapter 4.

Suppose that a scalar field $U$ describes an equilibrium temperature distribution in a room. Such a distribution is typically not uniform: it may be colder near a window and warmer near a radiator. Empirically, we know of this distribution that there cannot be a point inside the room that is, say, hotter than all of its immediate neighbors. If such a distribution were to occur in the absence of heat sources -- for example, a moment after a candle is extinguished -- the temperature would begin to average out until an equilibrium as achieved where, once again, no point is hotter than its neighbors. Thus, me may decide to model an equilibrium distribution as one where the temperature at each point is exactly the average of its neighbors in some precise mathematical sense. That precise sense can be provided by the Laplacian. In this Section, we will show that the Laplacian of $U$ captures the deviation between the value of $U$ at a point and the average of its values on a small sphere centered at that point. Thanks to this property, an equilibrium temperature distribution may be characterized by zero Laplacian, i.e. Functions whose Laplacian vanishes are known as harmonic and occupy an important place in applied mathematics. If a temperature distribution is not equilibrium, then its return to equilibrium is naturally modeled by the heat equation which essentially states the rate of change in temperature at a given point is proportional to its deviation from the average of its neighbors. This canonical example shows how this interpretation of the Laplacian leads to numerous physical applications.

Let us now derive the precise way in which the Laplacian captures the deviation between the value of $U$ at a point and the average of its values on a small sphere centered at that point. Consider a scalar field $U$ in a neighborhood of a point $P$ in a two-dimensional Euclidean space, i.e. a plane, where a sphere is replaced by a circle. Refer the plane to Cartesian coordinates $x,y$ with the point $P$ at the origin. Recall that in Cartesian coordinates, the Laplacian is given by the equation

In the vicinity of $P$, we can approximate the function $U\left( x,y\right)$ by the first two terms of its Taylor series, i.e. where all of the derivatives are evaluated at $P$.

Next, consider a circle of radius $r$ centered at $P$. If the circle is parameterized by the equations then the average $\left\langle U\right\rangle$ of the values of $U$ over the circle is given by the integral Substituting the Taylor series approximation for $U$ and evaluating the resulting integral, we find where we see the expression of the Laplacian emerging on the right. Indeed, the leading term in the difference between $\left\langle U\right\rangle$ and $U\left( 0,0\right)$ is directly proportional to the Laplacian, i.e. This equation captures the precise sense in which the Laplacian is a measure of the deviation between the value of a function and the average of its neighbors.

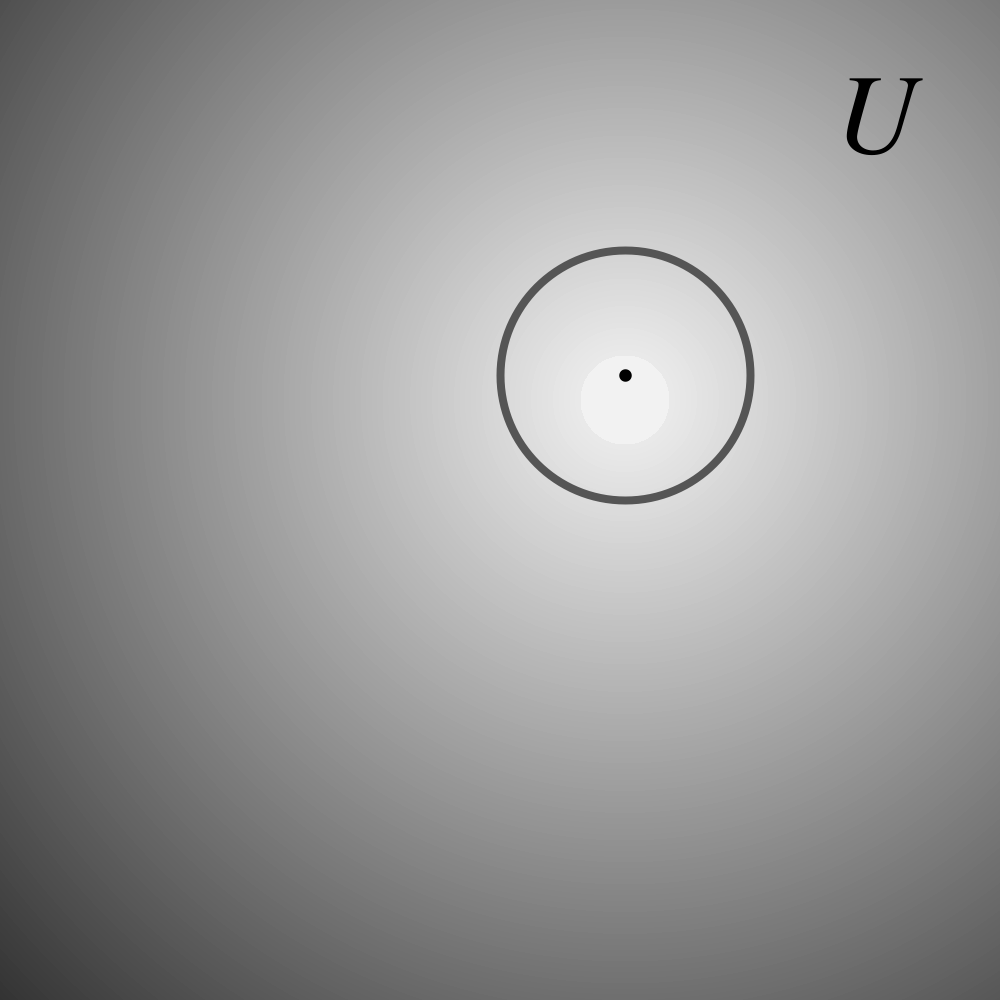
In the following figure, the function illustrated by the contour plot on the left is characterized by a small value of the Laplacian. By contrast, the function on the right has a high value of the Laplacian.

The geometric interpretation of divergence comes from the divergence theorem, a crucial generalization of the Fundamental Theorem of Calculus from one-dimensional intervals to higher-dimensional domains. The divergence theorem and its applications represent a vast topic that we will discuss in a future book. For the sake of the present discussion, however, we will give the statement of the theorem here.

Consider a closed domain $\Omega$ with boundary $S$ and outward unit normal $\mathbf{N}$ with components $N^{i}$. For a vector field $\mathbf{U}$ with components $U^{i}$, the divergence theorem reads In dyadic terms, the divergence theorem appears in the form The geometric interpretation of the divergence of $\mathbf{U}$ which we are currently pursuing can be gleaned from the integral on the right.

For simplicity, consider a uniform vector field $\mathbf{U}$ in the vicinity of a straight boundary $S$ characterized by the normal $\mathbf{N}$. This simple configuration will help us demonstrate that the dot product $\mathbf{U}\cdot\mathbf{N}$ corresponds to the flux of $\mathbf{U}$ across $S$, i.e. the rate at which the fluid mass crosses the interface. We will begin by considering the two extreme examples illustrated in the following figure. The left plot shows a flow parallel to the boundary $S$. In this case, no fluid crosses $S$ and therefore the flux is zero. Correspondingly, the dot product $\mathbf{U}\cdot\mathbf{N}$ vanishes and therefore so does the integral $\int_{S}\mathbf{U}\cdot\mathbf{N~}dS$. The right plot shows a flow orthogonal to the boundary, which results in the greatest flux. Correspondingly, $\mathbf{U}\cdot\mathbf{N}$ attains its maximum value, which equals the magnitude of $\mathbf{U}$, and the integral $\int_{S} \mathbf{U}\cdot\mathbf{N~}dS$ indeed corresponds to the rate at which the fluid mass crosses the interface $S$, i.e. the flux.

Finally, consider a flow with an angle of attack that equals $\gamma$ with respect to the normal $\mathbf{N}$. Identify a segment along the boundary of length $\Delta S$ and calculate the amount of fluid that crosses that segment in a period of time $\Delta t$. The fluid that crosses the segment in that time period is contained in the (gray) parallelogram with sides $\Delta S$ and $U\Delta t$, and an angle of $\pi/2-\gamma$. The total amount of fluid contained in this parallelogram corresponds to its area $A$ given by Thus, the amount of fluid crossing the segment per unit time and per unit length along the interface is Since $U\cos\gamma$ is precisely $\mathbf{U}\cdot\mathbf{N}$, we have Therefore, the integral represents the instantaneous amount per unit time of fluid crossing the boundary, which we understand to be the flux. More specifically, since $\mathbf{N}$ is the outward normal, the integral represents the instantaneous rate of fluid escaping the domain $\Omega$.

Thanks to the divergence theorem the volume integral also represents the instantaneous rate of fluid escaping the domain $\Omega$. In order to obtain an intuitive understanding of $\operatorname{div} \mathbf{U}$ in the local sense, consider a "small" domain $\Omega$ over which the field $\mathbf{U}$ is approximately linear and the quantity $\operatorname{div}\mathbf{U}$ is therefore approximately constant. If $\operatorname{div}\mathbf{U}$ is small then, correspondingly, the net flux across the closed boundary is also small. Such a flow may look like the one in the following plot.

If, on the other hand, $\operatorname{div}\mathbf{U}$ is large then we expect a large net flow across the boundary. If $\operatorname{div}\mathbf{U}\gt 0$, the corresponding flow may look like the one in the following plot. Of course, this is an exaggerated flow meant to illustrate the point. Nevertheless, these examples make it apparent where the divergence operator got its name.

In this Section, we will derive the expressions for the divergence and the Laplacian in the most common special coordinate systems.

Let us start with the divergence By definition, the covariant derivative $\nabla_{i}U^{j}$ is given by Contracting the indices yields the expression that is ready for interpretation in any coordinate system. For future convenience, let us switch the indices $i$ and $k$ in the second term, i.e.

Recall that we have encountered the combination $\Gamma_{ik}^{i}$ before in the equation which was later used to demonstrate the tensor property of the Levi-Civita symbols. Later in this Chapter, we will also use the above equation in the derivation of the Voss-Weyl formula which provides an alternative approach to calculating the divergence in any particular coordinate system.

Let us now begin to interpret the equation in various coordinate systems. In affine and, in particular, Cartesian, coordinates $x,y,z$, where the Christoffel symbols vanish, we have

In cylindrical coordinates, recall that the nonzero elements of the Christoffel symbol $\Gamma_{jk}^{i}$ are Consequently, the three elements of the contraction $\Gamma_{ki}^{k}$ are Therefore, the expression for the divergence in terms of the contravariant components reads Note that the first two terms can be effectively combined into a single term, i.e. The Voss-Weyl formula discussed later in this Chapter will clarify for us why the combination is a natural one.

It is left as an exercise to show that in polar coordinates in a two-dimensional Euclidean space, the divergence is given by the equation

Finally, let us turn our attention spherical coordinates. Recall that the nonzero elements of the Christoffel symbol $\Gamma_{jk}^{i}$ are and thus the three elements of $\Gamma_{ki}^{k}$ are As a result, in spherical coordinates, we have Analogously to the divergence, some of the terms can be combined, yielding the form which will, once again, be elucidated by the Voss-Weyl formula described below.

Since the contravariant derivative $\nabla^{i}U$ is given by the expression for the Laplacian in terms of the covariant derivatives alone reads Expanding the covariant derivatives in terms of partial derivatives, we find the form suitable for evaluation in various coordinate systems.

In Cartesian coordinates $x,y,z$, the Christoffel symbol vanishes and the metric tensors correspond to the identity matrix. Therefore, as we found before, we have In more general affine coordinates, the most specific form possible is where the elements of the contravariant metric tensor $Z^{ij}$ are constants.

In cylindrical coordinates $r,\theta,z$, recall that and that the nonzero elements of the Christoffel symbol are Since $Z^{ij}$ corresponds to a diagonal matrix, the only surviving terms in must have $i=j$. Combining these observations yields As before, the first two terms can be combined into one, leading to the final form

In spherical coordinates $r,\theta,\varphi$, recall that which is again diagonal, and that the nonzero elements of the Christoffel symbols $\Gamma_{ij}^{m}$ for which $i=j$ are Upon substituting these values into the equation and simplifying, we get where, combining terms as before, we arrive at the final form

In this Section, we are experiencing one important feature of tensor analysis. Namely, tensor expressions can be used to produce coordinate-dependent expressions directly, i.e. without a reference to another coordinate system. This feature is best characterized by the adjective absolute which was used in the original name of our subject, the Absolute Differential Calculus.

An alternative approach, used in virtually all introductory Calculus textbooks, is to define objects in the context of a Cartesian coordinate system and then to derive their expressions in other coordinate systems by a change of variables from the Cartesian coordinates. For example, the Laplacian would be defined by the expression in some Cartesian coordinates. Then it would be demonstrated that this expression yields the same value in all Cartesian coordinates. Finally, a (laborious and error-prone) change of variables from Cartesian to spherical coordinates would be used to derive the expression It is safe to say that, in this regard, the absolute approach of Tensor Calculus is superior. Furthermore, Tensor Calculus does not stop there. The Voss-Weyl formula, which we are about to describe, makes the Tensor Calculus approach even more efficient and robust.

The Voss-Weyl formula, named after Aurel Voss and Hermann Weyl, represents an alternative approach to calculating the divergence. It reads where $\sqrt{Z}$ is, of course, the volume element. The advantage of the Voss-Weyl formula is that provides a way of calculating the divergence, and therefore the Laplacian, without a reference to the Christoffel symbol.

To prove the Voss-Weyl formula, recall the formula for the divergence and the fact that we have encountered the combination $\Gamma_{ki}^{k}$ previously in the formula for the partial derivative of the volume element $\sqrt{Z}$. Solving for $\Gamma_{ki}^{k}$, we have Substituting this identity into the above formula for divergence, we find Upon factoring out $1/\sqrt{Z}$, we find where we observe, by (a reverse application of) the product rule, that the quantity in parentheses equals Thus we arrive at the desired result

A direct application of the Voss-Weyl formula to the Laplacian $\nabla _{i}\nabla^{i}U$ yields Since the contravariant derivative $\nabla^{i}U$ is given by the final expression for the Laplacian in terms of partial derivatives reads

The Voss-Weyl formula makes it an even simpler task to derive the expressions for the divergence and the Laplacian in special coordinate systems. For example, taking the most difficult example of spherical coordinates $r,\theta,\varphi$, recall that and that Since the above matrix is diagonal, the Laplacian is given by a sum of three terms, i.e. which leads directly to the final expression Note that the structure of the Voss-Weyl shows why combinations such as represent a natural way of grouping partial derivatives.

In summary, the Voss-Weyl formula offers an elegant way of evaluating the divergence, and therefore the Laplacian, with less effort while maintaining greater structure within the expressions.

We will now add the Levi-Civita symbols to the mix, which will give rise to the curl. Since the order of a Levi-Civita symbol depends on the dimension of the space, one obtains different kinds of objects in different dimensions. The classical curl is associated with three dimensions.

In a three-dimensional Euclidean space, consider a vector field $\mathbf{U}$ with components $U^{i}$. The curl of $\mathbf{U}$, dyadically denoted by $\operatorname{curl}\mathbf{U}$ or $\mathbf{\nabla}\times\mathbf{U}$, is given by The components $V^{k}$ of $\mathbf{V}=\operatorname{curl}\mathbf{U}$ are given by The invariant nature of the curl immediately follows from the fact that it is defined in terms of tensors and tensor-preserving operations. As always, we must note that the Levi-Civita symbol $\varepsilon^{ijk}$, as classically defined, is a tensor only with respect to orientation-preserving coordinate transformations. Therefore, the curl of $\mathbf{U}$, as defined by the above equations, is also a tensor only with respect to orientation-preserving coordinate transformations. It could be made a full tensor by introducing the orientation scalar $\Pi$, discussed in Section 17.10.

Interestingly, and perhaps somewhat unexpectedly, the covariant derivative $\nabla_{i}$ in the equation can be replaced with the partial derivative $\partial/\partial Z^{i}$. Indeed, recall that the Christoffel symbol is symmetric, i.e. and therefore as a double contraction of an alternating system with a symmetric system. Since we have Thus, as we set out to show.

A great mnemonic device for the curl can be formulated with the help of the determinant. Namely, the curl is given by the formula where it is understood that "multiplying" by the covariant derivative means applying it. Since, as we just discovered, the covariant derivatives can be replaced with partial derivatives, the above formula can be rewritten as We observe, therefore, the curl is given by the same expression in term of partial derivatives in all coordinate systems, save for the factor of $1/\sqrt{Z}$. Thus, there is no need for documenting the particular expressions for the curl in specific coordinate systems.

The geometric interpretation of the curl is that it is a local measure of swirliness in the vector field $\mathbf{U}$. Much like with the divergence, this interpretation comes from an integration theorem. Namely, Stokes' theorem which is a form of the divergence theorem that applies to a curved surface patch $S$ immersed in a vector field $\mathbf{U}$. It will be described, along with the divergence theorem, in a future book, but its statement will be given here for the purposes of our present discussion. 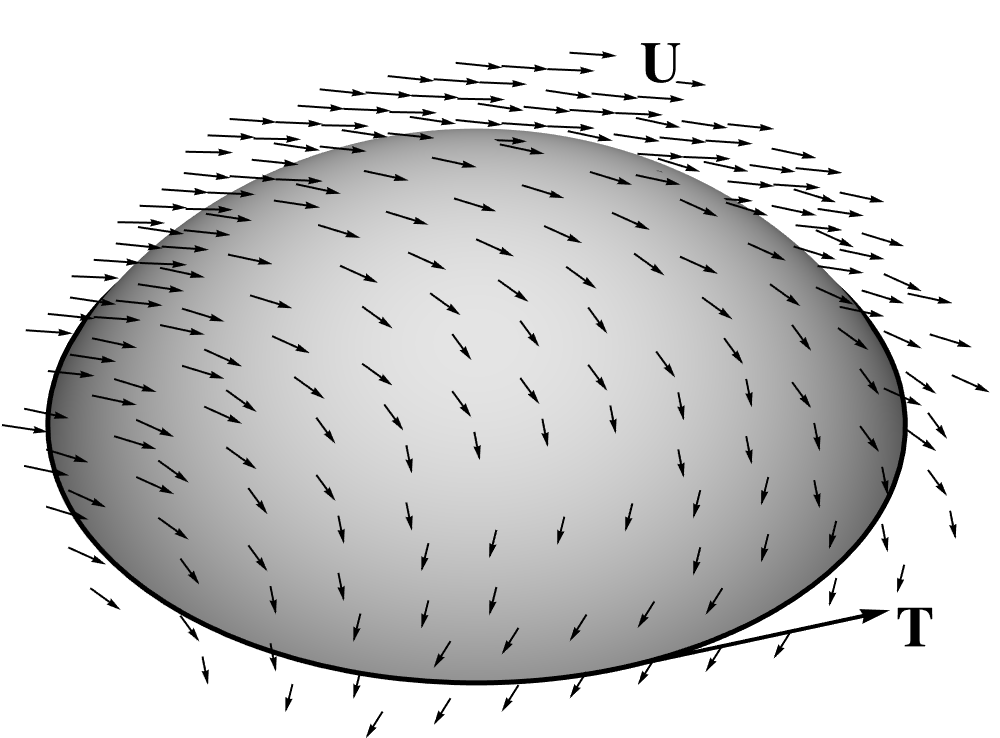If $\mathbf{N}$ is the unit normal on a patch $S$ and $\mathbf{T}$ is the unit tangent along the boundary $\Gamma$, then the Stokes' theorem reads As with the divergence, the interpretation of $\operatorname{curl}\mathbf{U}$ comes from the contour integral on the right as we consider a small patch.

In fact, let us consider a small circular patch $S$ and note that the tangent $\mathbf{T}$ exemplifies swirliness. At each point on the boundary $\Gamma$, the dot product $\mathbf{U} \cdot\mathbf{T}$ in the integrand of the contour integral $\int_{\Gamma }\mathbf{U}\cdot\mathbf{T~}d\Gamma$ is proportional to the magnitude of $\mathbf{U}$ and, importantly, to the cosine of the angle between $\mathbf{U}$ and $\mathbf{T}$, i.e. the degree to which $\mathbf{U}$ is aligned with $\mathbf{T}$. Thus, the contour integral rewards the "likeness" between $\mathbf{U}$ and $\mathbf{T}$ and thus rewards the swirliness in $\mathbf{U}$.

Suppose that the space is referred to Cartesian coordinates so that the circle patch $S$ is in the $x$-$y$ and with its center at the origin. Consider the three different vector fields given by the equations and illustrated in the following figure. It is left as an exercise to show that

Due to the swirly character of the vector field $\mathbf{U}_{1}$ in the first plot, we observe that along the boundary, $\mathbf{U}$ and $\mathbf{T}$ are consistently aligned. As a result, the dot product $\mathbf{U}\cdot\mathbf{T}$ is positive everywhere and every point makes a positive contribution to the integral $\int_{\Gamma}\mathbf{U}\cdot\mathbf{T~}d\Gamma$.

Meanwhile, in the other two plots, $\mathbf{U}$ fails to exhibit any degree swirliness. In the second plot, $\mathbf{U}$ is orthogonal to $\mathbf{T}$ at each point resulting in the zero contour integral. In the third plot, $\mathbf{U}$ varies from being largely aligned with $\mathbf{T}$ at some points to counter-aligned at other points. Consequently, the contributions to the contour integral from the different sections of the boundary cancel each other, once again resulting in a zero integral.

As a final remark, note that swirliness may be difficult to judge with the naked eye. For example, even the swirly field in the first plot does not appear swirly away from the origin. However, it is equally swirly at all points, as indicated by the constant value of $\operatorname{curl}\mathbf{U}$. In order for the swirliness to become visually apparent on a small patch, one needs to subtract out the average value of the field.

In a two-dimensional space, the Levi-Civita symbol $\varepsilon^{ij}$ has two indices and, thus, there are not enough indices to produce a first-order tensor out of the combination $\nabla_{i}U_{j}$. Nevertheless, we can still consider the combination $\varepsilon^{ij}\nabla_{i}U_{j}$ which produces a scalar invariant $V$, i.e. As in the case of the three-dimensional curl, the covariant derivatives can be replaced with partial derivatives and the result can be captured by the determinant equation

Much like the curl in three dimensions, $V$ measures the degree of swirliness in the field $\mathbf{U}$. For the vector field which exemplifies swirliness, $V$ is given by

The identities of Vector Calculus are rarely used in all but the most elementary applications. Most analyses encounter situations not covered by the common Vector Calculus identities involving $\operatorname{grad}$, $\operatorname{div}$, $\operatorname{curl}$ and the Laplacian. As we already discussed, even the analysis of a combination as fundamental as $\mathbf{\nabla}\left( \mathbf{U}\cdot\mathbf{V}\right)$ requires the introduction of new operators. Thus, at best, the Vector Calculus identities are incomplete.

In Tensor Calculus, the need for analogous identities simply does not arise. All analyses are built up from the metrics and the covariant derivative, and proceed according to the limited set of rules governing the handful of available operations. It is certainly true that any analysis will reference previously established relationships, such as However, using such relationships is simply a matter of convenience since all such relationships can be derived from first principles by the same limited set of rules. In other words, none of these relationships can be considered primary in the sense that they must be a priori derived by means outside of the present framework. Thus, every analysis in Tensor Calculus can, and often does, proceed from first principles and is guaranteed not to encounter a combination, such as $\mathbf{\nabla}\left( \mathbf{U} \cdot\mathbf{V}\right)$ in Vector Calculus, that cannot be reduced to already-available more primary objects. Ultimately, every analysis in a Euclidean space can be performed in terms of the covariant derivative and the metrics, which, in turn, can be expressed in terms of partial derivatives and the position vector. (In a Riemannian space, the covariant metric tensor replaces the position vector as the primary object and therefore every analysis can be reduced to partial derivatives and the metric tensor.)

Nevertheless, for illustrative purposes, we would like to use the techniques of Tensor Calculus to demonstrate some of the most common identities of Vector Calculus, such as Other identities that may be stated in dyadic terms but whose proof requires coordinate-based calculations, are left as exercises for the reader.

Let us begin with the first two identities and show that both follow easily from the skew-symmetric property of the Levi-Civita symbol. Since the components of $\operatorname{grad}U$ are $\nabla_{j}U$, the components of $\operatorname{curl}\operatorname{grad}U$ are

varepsilon^{ijk}nabla_{i}nabla_{j}U. Recall that, in a Euclidean space, the covariant derivatives commute, i.e. nabla_{i}nabla_{j}U=nabla_{j}nabla_{i}U. Consequently, the preceding expression represents a double contraction between a skew-symmetric system, $\varepsilon^{ijk}$, and a symmetric system, $\nabla_{i}\nabla_{j}U$, and therefore vanishes, as we set out to show.

Turning our attention now to $\operatorname{div}\operatorname{curl}\mathbf{U}$, the components of $\operatorname{curl}\mathbf{U}$ are $\varepsilon ^{ijk}\nabla_{i}U_{j}$ and therefore $\operatorname{div}\operatorname{curl} \mathbf{U}$ is given by the expression By the metrinilic property, the Levi-Civita symbol "passes through" the covariant derivative, i.e. and we once again have a double contraction (on $i$ and $k$) between a skew-symmetric system, $\varepsilon^{ijk}$, and a symmetric system, $\nabla_{k}\nabla_{i}U_{j}$. Therefore, the result is zero as we set out to show.

Finally, let us consider $\operatorname{curl}\operatorname{curl}\mathbf{U}$, which will lead to a more intricate analysis. Let The components $V^{k}$ of $\mathbf{V}$ are given by Thus, the components $W_{s}$ of $\mathbf{W}$ are given by Once again, the Levi-Civita symbol "passes through" the covariant derivative $\nabla^{r}$, i.e. The combination $\varepsilon_{rks}\varepsilon^{ijk}$ is given by as it is left as an exercise to show. Therefore, Upon applying the distributive law and absorbing the Kronecker symbols, we find Finally, switching the order of the covariant derivatives in each term (for largely aesthetic reasons), we arrive at the final expression Expressed in dyadic terms, the above identity reads as we set out to show.