9.1Introductory remarks
Curves embedded in surfaces present us with a fascinating interplay among three spaces: the curve
itself, its ambient surface, and the overall Euclidean space. There are also three embeddings to
consider, i.e. that of the surface within the Euclidean space, of the curve within the Euclidean
space, and, finally and most interestingly, of the curve within the surface. Although our interest
is in all three embeddings and their interplay, it is the last embedding that is new to us and will
therefore receive the greatest amount of attention.  (9.1)
(9.1)
 (9.1)
(9.1)Each embedding has a curvature tensor associated with it. The embedding of the surface within the
Euclidean space is characterized by the now-familiar curvature tensor .
The embedding of the curve within the Euclidean space is characterized by the vector curvature
tensor
introduced in the previous Chapter. Finally, the embedding of the curve within the surface is
characterized by the geodesic curvature tensor , which
will be introduced in this Chapter. The geodesic curvature tensor is
entirely analogous to the curvature tensor
and the term geodesic simply refers to the fact that
characterizes the embedding of the curve within the surface.
It is intuitively clear that the three curvature tensors are related. After all, if a surface is
curved then it may not be able to accommodate straight curves, at least in some directions. Thus,
high values in the curvature tensor
may induce relatively high values in the vector curvature tensor
depending on the orientation of the curve within the surface. This insight is reflected in the
formula
where is
the shift tensor of the curve with respect to the surface and is the unit normal to the curve within the surface. This
formula is the culmination of this Chapter and may be interpreted as the attribution of the curve's
overall curvature characteristics (captured ) to
the curvature of the surface (captured by )
and the curvature of the curve within the surface (captured by ).
Finally, we will continue to use the tensor notation with uppercase Greek letters for curve
indices, despite the fact that curves are one-dimensional objects. In addition to the advantages
mentioned in the previous Chapter, the analysis presented in this Chapter will benefit from this
approach in one more important way. Namely, in higher-dimensional spaces, whether artificial
Euclidean or Riemannian, one can consider similar curve-surface-space embeddings where the "curve",
i.e. the innermost object, is of dimension greater than one. Thanks to our present use of the
tensor notation to describe embedded curves, most of our analysis will generalize easily to those
situations.
9.2The taxonomy of the embeddings and coordinate systems
In order to describe a curve embedded in a surface which is, in turn, embedded in a Euclidean space
we must introduce three coordinate systems: on
the curve,
on the surface, and in
the ambient space. It is somewhat of a problem that the curve and surface coordinates are denoted
by the same letter . For instance, the symbol is
ambiguous as it simultaneously stands for the curve coordinate and the first surface coordinate.
However, we will typically refer to the coordinates collectively either by or by
so this potential ambiguity will be avoided. As we are about to see, the only real problem
momentarily arises in the vector equations of the surface and the curve. 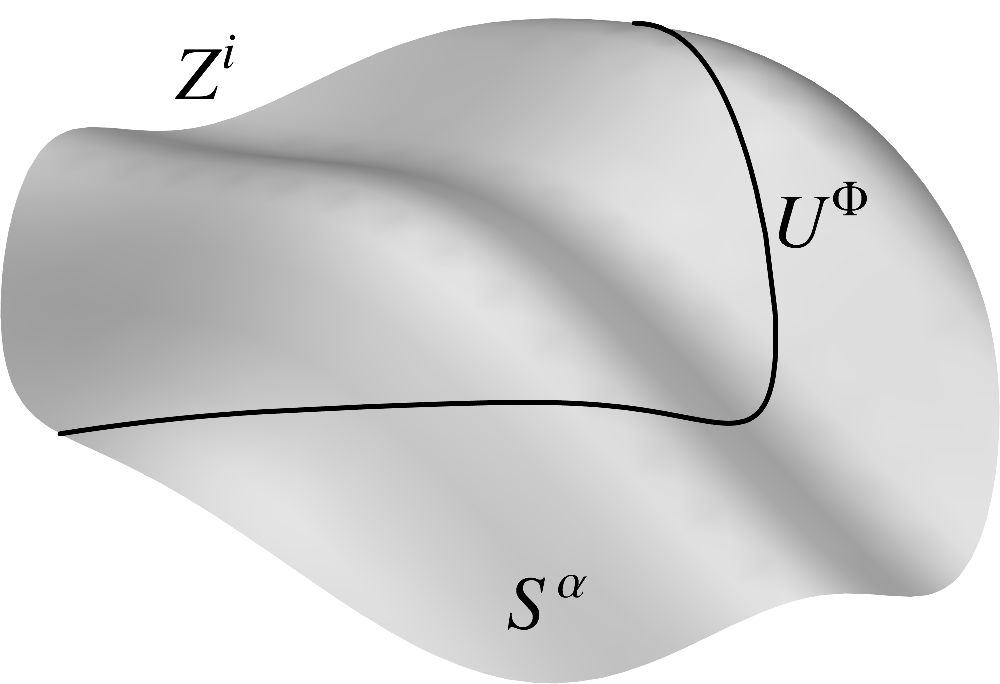 (9.2)
(9.2)
 (9.2)
(9.2)Denote the dependence of the position vector on the ambient coordinates by
the familiar function . Let the vector equations of the surface be
denoted by the function . Finally, the vector equations of the curve
will also be denoted by since both the curve and the surface
coordinates are represented by the same letter . This is the momentary problem we
have just alluded to in the previous paragraph. However, this problem is indeed only momentary
since we never discuss the vector equations themselves but, rather, their derivatives with respect
to the coordinates which produce the respective covariant bases , , and
.
Those bases are given by familiar equations
Note that in the last equation, the superscript of in
the "denominator" makes it clear in the "numerator" represents the vector
equation of the curve.
Each of the objects above is well familiar to us from the earlier Chapters, along with the other
fundamental objects that are constructed from them, such as the metric tensors, the contravariant
bases, the volume, area, and length elements, the Levi-Civita symbols, the Christoffel symbols, and
the Riemann-Christoffel tensors. Furthermore, we have also established relationships between the
ambient and surface objects, as well as between the ambient and curve objects. However, we are yet
to discuss the corresponding relationships between the surface and the curve objects, which is
precisely the task to which we will now turn our attention.
9.3The interplay between the equations of the surface and the curve
The shape of a curve embedded in a surface can be described by the relationship between the curve
coordinates and
the surface coordinates .
The resulting equations
are called the geodesic equations
of the curve. In and of themselves, the geodesic equations of the curve do not carry the
complete information about the overall shape of the curve in the three-dimensional space. In order
to get the full picture, the geodesic equations need to be combined with the equation of the
surface
When these equations are composed,
the result is, of course, the equations of the curve in the three-dimensional space,
i.e.
This identity can be readily
differentiated with respect to by
applying the chain rule on the right. We have
Of course, we are already familiar
with the shift tensor
that characterizes the embedding of
the curve in the ambient space, as well as the shift tensor
that characterizes the embedding of
the surfaces in the ambient space. The only new element in the identity
is object
associated with the embedding of the curve within the surface. This object is denoted by ,
i.e.
and is also referred to as a
shift tensor, although it may also be referred to as the geodesic shift tensor.
The three shift tensors ,
, and
are related by the identity
This identity does not have an
official name, but it is well described as cascading projections. Recall from Chapter 3 that
represents projection from the ambient three-dimensional space onto the surface. Similarly,
represents projection from the ambient space onto the curve and
represents projection from the tangent plane onto the curve. The identity
tells us that projection from the
space onto the curve is equivalent to projection from the space onto the surface followed by
projection onto the curve. Our derivation may have been straightforward, but this is actually a
nontrivial geometric result.
Next, let us convert the relationship
among the shift tensors into a
relationship between the curve and surface covariant bases. To this end, contract both sides of the
above with the ambient basis , i.e.
Since and
, we
arrive at the relationship
which, given our accumulated
experience, we could have all but predicted. And we can also predict that a differentiation of this
identity will yield a relationship among the various characteristics of curvature.
Meanwhile, the equation
yields the relationship between the
curve and the surface metric tensors, i.e.
The equivalent forms of this
identity are
and
9.4The geodesic normal
Since the embedded curve is a hypersurface with respect to the ambient surface, it has a
well-defined, to within sign, unit normal that lies in the tangent plane to the surface. 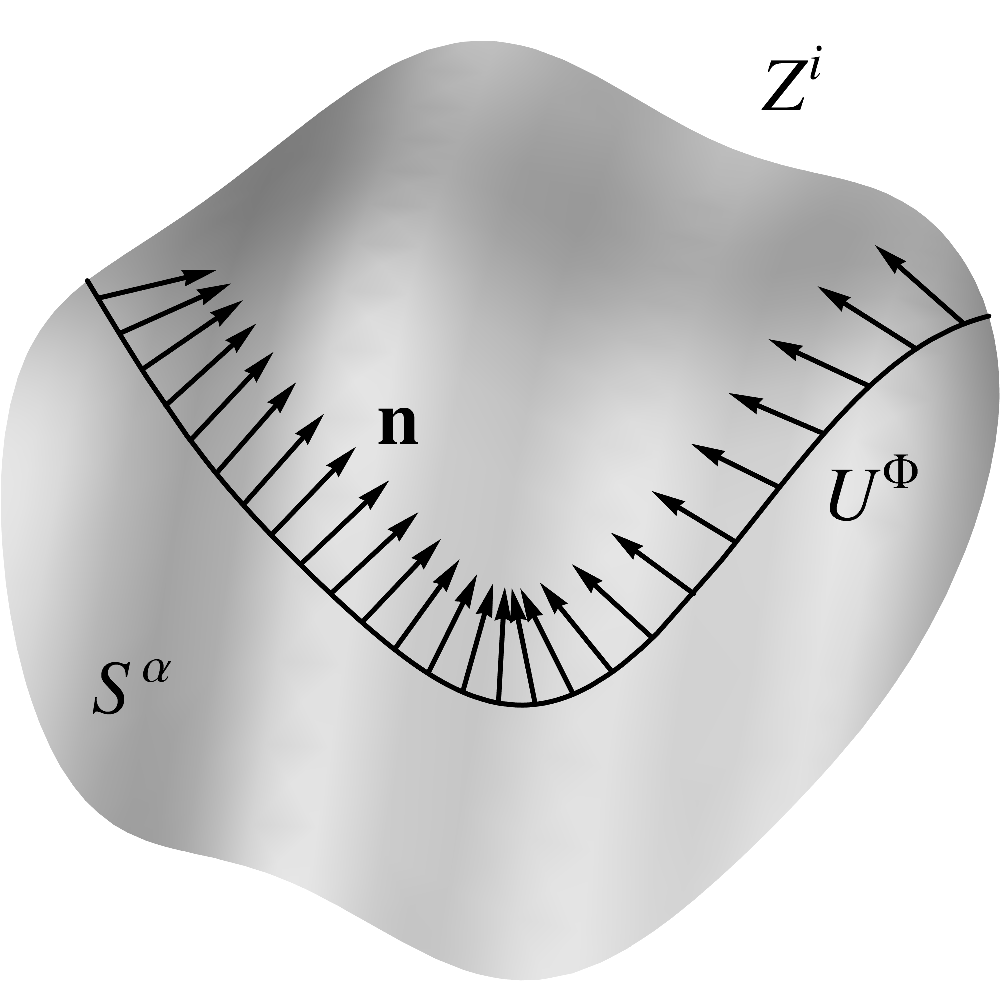 (9.19) We will call the geodesic normal. It is specified uniquely, to
within sign, by the condition that it lies in the tangent plane, is orthogonal to textbf{}, i.e.
(9.19) We will call the geodesic normal. It is specified uniquely, to
within sign, by the condition that it lies in the tangent plane, is orthogonal to textbf{}, i.e.
 (9.19)
(9.19) and that it has unit length, i.e.
Denoting the components of with respect to the surface basis by
,
i.e.
the above conditions read
and
The explicit expression for ,
analogous to its classical counterpart
for the components of the surface
normal , reads
Naturally, it exhibits the same
limitations: the resulting variant may differ in sign from the components of an a priori choice of
normal. Furthermore, the quantity on the right is a tensor only with respect to the
orientation-preserving coordinate changes.
The geodesic normal can also be decomposed with respect to the ambient basis
, i.e.
Since the ambient components of a
vector are obtained by contracting its surface components with the shift tensor , i.e.
we have
and therefore
9.5The geodesic projection formula
The projection formula
first derived in Chapter 2, demonstrates that a vector on the surface, can be represented as a sum of its tangential
and normal projections, and
. In component form, the projection formula reads
Naturally, an analogous formula exists for curves embedded in surfaces. It features the curve
covariant basis textbf{} and
the geodesic normal and applies to vectors in the tangent plane. Specifically,
for a vector in tangent plane, we have
where the terms and
are interpreted as the components of that are tangential and orthogonal to the curve. The
component form of the same equation reads
which is usually applied in the form
whenever the combination
is encountered.
Similarly to the object
discussed in Chapter 3,
represents orthogonal projection from the tangent space of the surface to the tangent space of the
curve. Also recall from Chapter 8, that the shift
tensor is
proportional to the ambient components of
the unit tangent . In fact,
Similarly, the shift tensor is
proportional to the surface components
of , where
Since the combination
also represents orthogonal projection from the tangent space of the surface to the tangent space of
the curve, we should expect that
The simplest way to demonstrate this
identity is to note that, similarly to the identity
we have
Thus, recalling that ,
we have
as we set out to show.
9.6The covariant derivative
We have already defined the curve covariant derivative for
objects and ambient and curve indices. We must now extend it to surface
indices. This can be accomplished according to the well established blueprint. However, rather than
give an overwhelming expression for a variant
with a fully representative collection of indices, we will give three separate expressions for
,
,
since the tactic of the definition is simply to indicate the proper treatment of each kind of
index. We have:
By now, we have significant experience constructing differential operators that possess the tensor
property along with a slew of other desirable characteristics. We will therefore limit ourselves to
stating the definition and assume that the reader will fill in all of the necessary details.
For a variant
defined in the ambient Euclidean space,
satisfies the chain rule
while for a variant
defined in the wider ambient surface outside,
satisfies the chain rule
As a result, is
metrinilic with respect to all of the ambient metrics, including the covariant and contravariant
bases and
.
However, while is
metrinilic with respect to the scalar surface metrics, we are not able to conclude the same with
respect to the surface covariant and contravariant bases and
due to the lack of the metrinilic property of the surface covariant derivative with
respect to those objects. Indeed, since
we have, by the chain rule
Let us now summarize the results of
applying the curve covariant derivative to the ambient, surface, and curve bases:
where is the
vector curvature tensor introduced in the preceding Chapter.
The above expressions bring us face to face with the analysis of curvature which is the task to
which we now turn.
9.7Geodesic curvature
9.7.1The intuition behind geodesic curvature
The purpose of geodesic curvature is to characterize the shape of an embedded curve relative to the
ambient surface. This concept is exemplified by the difference between roads that we would
differentiate as straight and curved.  (9.47)
(9.47)
 (9.47)
(9.47)Naturally, even the "straight" road in the picture above is not straight in the absolute sense
since it curves with the curvature of the Earth. However, on an intuitive level, it is "as straight
as possible" given that it is constrained to follow the surface of the Earth. We might describe it
as straight relative to the surface of the Earth. Such roads also correspond to our
intuitive understanding of what it takes to connect two towns by the shortest possible path.  (9.48) The road in the second picture, on the other hand, would be
described as curved relative to the surface of the Earth. We will wish to design the
geodesic curvature tensor so that it is low -- ideally, zero -- for the "straight" road and high
for the other road. Notice, then, that it is its geodesic curvature that makes a road potentially
more dangerous and thus necessitates a lower speed limit -- curvature corresponds to acceleration
-- and a double yellow separator line.
(9.48) The road in the second picture, on the other hand, would be
described as curved relative to the surface of the Earth. We will wish to design the
geodesic curvature tensor so that it is low -- ideally, zero -- for the "straight" road and high
for the other road. Notice, then, that it is its geodesic curvature that makes a road potentially
more dangerous and thus necessitates a lower speed limit -- curvature corresponds to acceleration
-- and a double yellow separator line.
 (9.48)
(9.48)9.7.2The geodesic curvature tensor
Let us proceed by analogy with the classical curvature tensor
which characterizes a surface embedded in a Euclidean space. Recall its definition
By dotting both sides with the
surface normal we obtain an explicit expression for ,
i.e.
An analogous definition for the
geodesic curvature tensor would
read
However, this definition is flawed.
Indeed, while the vector is
orthogonal to the embedded curve, it is not necessarily found in the tangent plane and is therefore
not necessarily proportional to the geodesic normal . As a result, we will look to the equation
for the analogy and define the geodesic curvature tensor by the
equation
or, equivalently
The tensor thus
defined is called the geodesic curvature tensor.
Observe, crucially, that the vector curvature tensor is
characteristic strictly of the curve's embedding in the overall Euclidean space and has nothing to
do with the ambient surface. Thus, the dependence of the geodesic curvature tensor on the surface
enters strictly through the normal , i.e. the direction of the curve relative to the surface.
The invariant
is known as the geodesic
curvature although, perhaps, it would have been better described as the geodesic mean
curvature. It can be expressed as the dot product of the geodesic normal and the curvature normal ,
i.e.
In other words, it is the projection
of the curvature normal onto the geodesic normal. Thus, the geodesic curvature cannot exceed the
absolute curvature , i.e.
Recall from Chapter 8, that is defined as the magnitude of the
curvature normal .
Furthermore the geodesic curvature vanishes when the curvature normal is
orthogonal to the geodesic normal .
9.7.3A circle on the surface of a sphere
A great deal of geometric intuition about geodesic curvature and its relationship to the curvature
normal can be gained by considering circles on the surface of a sphere. The following figure shows
three parallel circles of different radii. For these circles, is
easy to visualize as it lies in the same plane as the circle and has magnitude that is the
reciprocal of the radius. Thus, for a small circle, which we would perceive as highly
curved, is
closely aligned with . For a large circle is
nearly orthogonal to .
A great circle is a circle on the surface of the sphere with the greatest possible radius
which, of course, equals the radius of the sphere itself. It has the property that its center is
located at the center of the sphere. In other words, a great circle is the intersection of the
sphere with a plane passing through its center. Consequently, its curvature normal is
orthogonal to the surface of the sphere and is therefore orthogonal to . As a result, the geodesic curvature
vanishes, i.e. . Note that it is intuitively clear that a "straight"
road on the surface of the Earth follows a great circle. 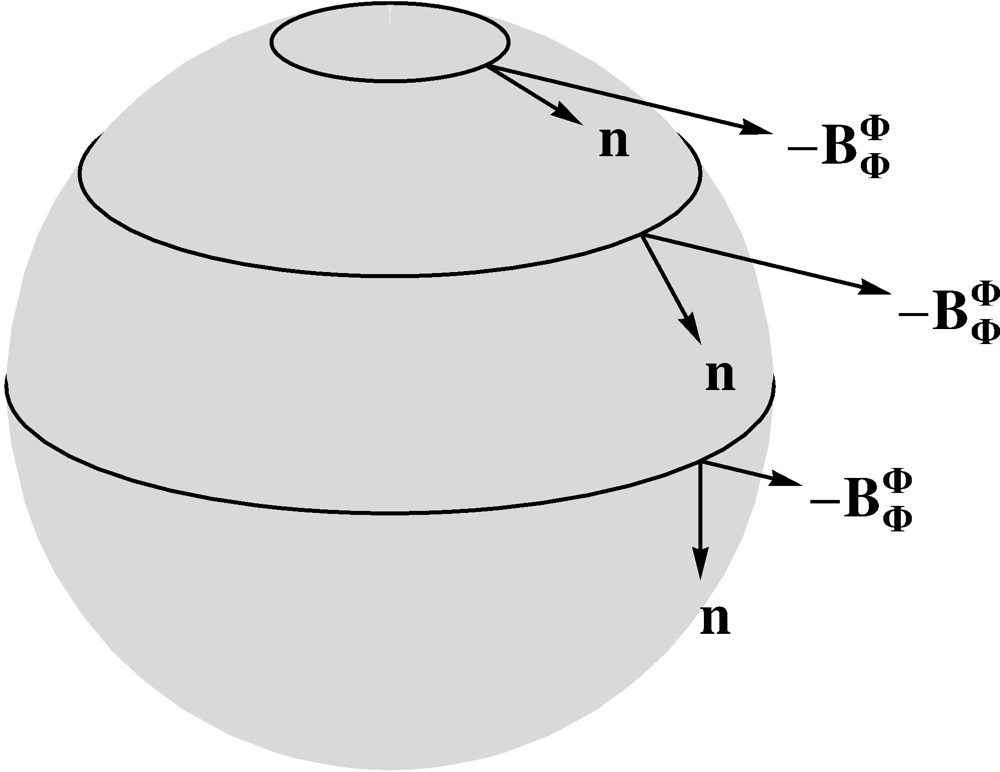 (9.54)
(9.54)
 (9.54)
(9.54)In fact, let us determine the actual value of the geodesic curvature of a circle of radius on the surface of a sphere of radius
. This configuration is illustrated in
the following figure.  (9.55) Since
(9.55) Since
 (9.55)
(9.55) while
we have
or, equivalently,
Note that this formula was derived
without introducing any surface or ambient coordinates, even though the angle is reminiscent of the longitudinal
angle in spherical coordinates.
According to the above formula
vanishes when which confirms our intuition that a
great circle is straight relative to the sphere. Also, when is small, we have
which tells us that the geodesic
curvature of a small circle essentially matches its absolute curvature and is independent of the
radius of the sphere. Finally, note that the sign of the geodesic curvature depends on the a
priori choice of the geodesic normal . Had we chosen the opposite direction of , all of the values of
would have had the opposite sign.
9.7.4The coordinate space expression for the geodesic curvature tensor
A shortcoming of the definition
is that it involves a quantity --
namely, the vector curvature tensor --
which is connected with the embedding of the curve in the overall three-dimensional Euclidean
space. Meanwhile, the goal of the geodesic curvature tensor is, of
course, to characterize the shape of the curve relative to the ambient surface. We would therefore
like to obtain an expression for
strictly in terms of the equations of the curve
and their derivatives.
Let us think back to the classical curvature tensor
and its coordinate space expression
The analogous equation for the
geodesic curvature tensor reads
however, at this point it is not
clear whether this definition is equivalent to the one we have already made. In the next Section,
we will show that it is indeed equivalent, and will also show the surprising identity
It is surprising because, as we have
already discussed, does
not hold.
The geodesic curvature is
given by the equation
A more general form of this equation
is
9.8The equation of the three curvatures
Let us go back to the analysis of the equation
that defines the vector curvature
tensor .
Notice that we can engage the geometry of the surface by substituting the previously obtained
expression for textbf{} in
terms of the surface basis , i.e.
By the product rule, the identity
becomes
As we discovered earlier, is
given by the equation
Thus, we have arrived at the
powerful identity
which represents a decomposition of
the vector curvature tensor into
its normal and tangential components with respect to the surface. The normal component
will be analyzed shortly. At the present time, let us direct our attention to the tangential
components .
As we discussed in the previous Section, we hope that the quantity is
related to the geodesic curvature tensor . This
is indeed easily seen to be the case by dotting both sides of the equation
with the geodesic normal , i.e.
The dot product on the
left is the geodesic curvature tensor .
Additionally, , and . Thus,
is
given by
as was our hope.
However, as we have already mentioned, we can demonstrate the stronger relationship
Indeed, since in the equation
both and
are orthogonal to the curve, we can conclude that
is, too, orthogonal to the curve. Since, at the same time,
lies in the tangent plane, it must be a scalar multiple of the geodesic normal . In other words,
for some .
Dotting both sides with proves that and
thus
From this identity, it immediately
follows that
as we set out to show. A more
algebraic proof of this identity can be found in one of the exercises.
With this newly obtained expression for ,
the equation
becomes
Since , we arrive at the beautiful identity
which captures the interplay between
the three curvature tensors , ,
and . We
will, therefore, refer to this identity as the equation of the three curvature tensors. To
summarize the roles of these tensors one more time, the vector curvature tensor
characterizes the shape of the curve relative to the Euclidean space, the classical curvature
tensor
characterizes the shape of the surface relative to the Euclidean space, and the geodesic curvature
tensor
characterizes the shape of the curve relative to the surface.
Raising the index in the equation
and subsequently contracting on
and (as well as juggling ) yields the stunning formula
that relates five invariants:
the curvature normal ,
the invariant
known as the normal curvature and discussed below, the geodesic curvature ,
the surface normal and the geodesic normal . It is fair to say that it is rare for a fundamental formula
to relate as many as five invariants. Interestingly, we can increase that number to six if we
replace the curvature normal with the product of the absolute curvature and the principal normal , i.e.
9.9The normal curvature
9.9.1The definition
The invariant
in the equation
is known as the normal
curvature. Since the shift tensor
depends only on the direction of the curve within the surface, the normal curvature is dictated
solely by the curvature characteristics of the ambient surface and the direction of the curve.
Also, since the sign of the curvature tensor depends on the choice of the surface normal , the same is true for the normal curvature.
There are two alternative expressions for the normal curvature that are free of curve indices.
First, with the help of the geodesic projection formula
we obtain an identity that features
the mean curvature , i.e.
Alternatively, with the help of the
identity
where
are the components of the unit tangent , we obtain an expression for the normal curvature
that is a simple quadratic form in
.
Recall from Chapter TBD in Introduction to Tensor Calculus, that the largest and the
smallest values of
equal the eigenvalues of ,
i.e. the principal curvatures and
.
We can now rewrite the equation of the three curvature tensors
and the equation of the three
curvatures
in the forms
and
or, equivalently,
By the Pythagorean theorem, the
absolute, normal, and geodesic curvatures are related by the equation
The last equation is illustrated in the following diagram, which shows the unit vectors , , and in the plane orthogonal to the curve. The vectors , are orthogonal to each other, while may be oriented in an arbitrary way with respect to them.
 (9.82)
(9.82)
 (9.82)
(9.82)9.9.2On the surface of a sphere
The normal curvature on the surface of a sphere is the same for all curves at all points. If the
radius of the sphere is , then the common value of normal
curvature with respect to the outward normal is . To show this, recall that on the
surface of a sphere the curvature tensor is related to the metric tensor by the identity
Therefore,
Finally, since
are the components of a unit vector, we have
as we set out to show.
Thus, on the surface of a sphere of radius , the equation of three curvatures
reads
and therefore the absolute curvature
satisfies the identity
If the curve is a circle of radius , then the above equation becomes
which is consistent with our earlier analysis of geodesic curvature of a circle on the surface of a
sphere.
9.10Meusnier's theorem
Suppose that a surface is cut by a plane at a point and consider a curve that arises at the intersection of
the surface and the plane. Meusnier's theorem, named after the French mathematician Jean Baptiste
Meusnier, states that the absolute curvature of the resulting curve at the point
depends only on the curvature tensor
and the orientation of the plane. 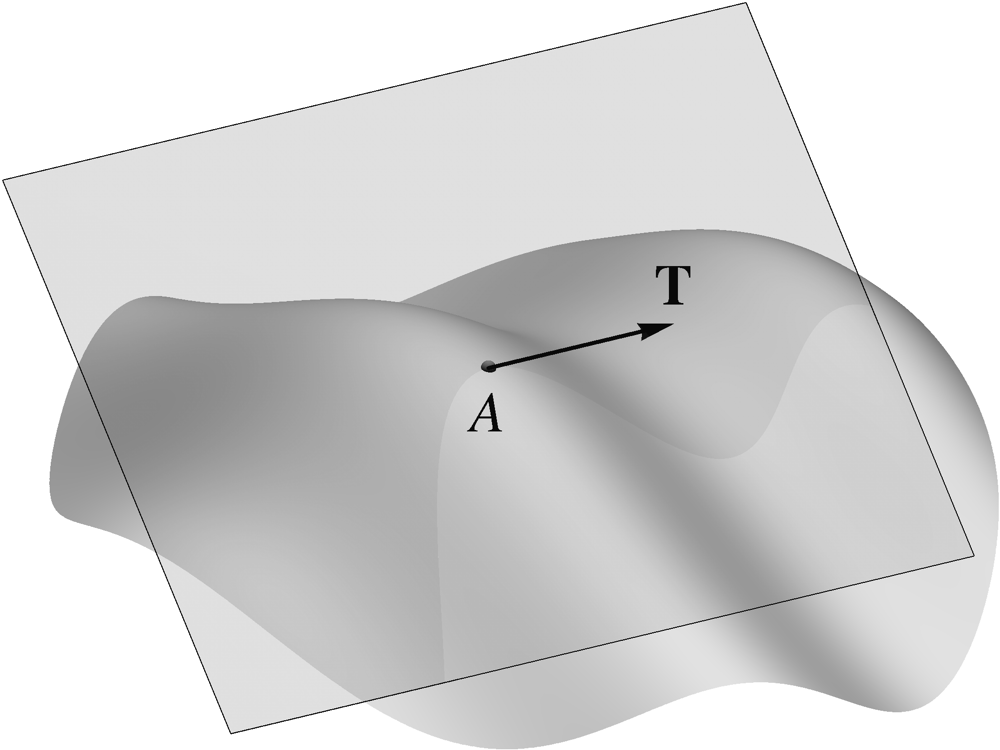 (9.89)
(9.89)
 (9.89)
(9.89)The analytical portion of Meusnier's theorem follows from the equations of the three curvatures
Dotting both sides with the surface
normal yields
In other words,
Note that the curve's unit tangent
and its principal normal both lie in the cutting plane and therefore determine its
orientation. Therefore, the right side in the above identity indeed depends only on the curvature
tensor and the orientation of the surface. Also note that the right side is independent of the
choice of the surface normal since both
and change their sign when the choice is reversed.
If is the angle between the principal
normal and the surface normal , then the above formula reads
This is the usual form in which Meusnier's theorem appears. In particular, if the cutting plane
contains the surface normal then the absolute curvature matches
the normal curvature up to sign, i.e.
Meusnier's theorem has a very striking geometric interpretation for which we need to introduce the
concept of an osculating circle for a planar curve. At a given point on a planar curve, the osculating circle is a
circle that passes through , and has the same tangent and curvature as the curve.
Analytically speaking, the curve and the circle agree in the first and second derivatives. The radius of the circle, i.e. the reciprocal of the absolute curvature, is referred to as
the radius of curvature for the curve at the point . Meanwhile, the center of the circle is referred to as
the center of curvature.
Now, consider a family of cutting planes passing through the point that share an axis containing the tangent vector .  (9.95) All of the resulting curves pass through the point and share the tangent . Since the curves share a common tangent direction, they all
have the same normal curvature .
Let us choose the surface normal so that
is negative and denote
by , i.e.
(9.95) All of the resulting curves pass through the point and share the tangent . Since the curves share a common tangent direction, they all
have the same normal curvature .
Let us choose the surface normal so that
is negative and denote
by , i.e.
 (9.95)
(9.95) Then the absolute curvatures of the
resulting curves are given by
where is, once again, the angle between the
principal normal and the surface normal .
Observe that these are the very absolute curvatures we would observe if our surface was a sphere of
radius and, correspondingly, the curves
arising as the result of the planar cuts were circles, as in the following figure.  (9.98) The fact that the absolute curvatures of the circles satisfy
the equation
(9.98) The fact that the absolute curvatures of the circles satisfy
the equation 
 (9.100) Thus,
returning to our actual surface, if each of the curves is replaced with its osculating circle the
collection of the circles will form a sphere of radius .
(9.100) Thus,
returning to our actual surface, if each of the curves is replaced with its osculating circle the
collection of the circles will form a sphere of radius .
 (9.98)
(9.98) can be seen in the following diagram
which shows that orthogonal cross-section of the sphere.

 (9.100)
(9.100)9.11Weingarten's equation for the geodesic normal
Recall Weingarten's equation
for the surface covariant derivative
of the normal . The component form of Weingarten's equation reads
Let us derive the analogous
equations for the geodesic normal .
For reasons that will become apparent shortly, we will first present the component form of
Weingarten's equation which reads
Thus, its form is entirely analogous
to its classical counterpart. Since the same is true for its derivation, we will leave it as an
exercise.
The vector form of Weingarten's equation, on the other hand, is fundamentally different from its
classical counterpart, owing to the lack of the metrinilic property of with
respect to the surface basis .
Indeed, differentiating both sides of
we find
Recall that
Thus,
and, equivalently,
The surprising aspect of the formula
is that, unlike its component form, it is more complicated than its classical counterpart. Of
course, this is an artifact of the curvature of the ambient surface which is captured by the term
containing the curvature tensor.
9.12Exercises
Exercise 9.1From the equation
show that
as well as the equivalent forms
and
Exercise 9.2Show that given by
satisfies the equations and .
Exercise 9.3Using the approach introduced in Chapter 2 for the proof of the projection formula
prove the geodesic projection formula
and establish its component form
Exercise 9.4Prove the component form
of the geodesic projection formula from the explicit expression
for the components of the geodesic normal.
Exercise 9.5Derive the equation
from
by dotting both sides with to obtain
Then obtain the desired result, by contracting both sides with and applying the geodesic projection formula.
Exercise 9.6Derive Weingarten's equation for the geodesic normal, i.e.
Exercise 9.7Consider a curve on the surface of a sphere of radius referred to spherical coordinates given by equations
Show that its geodesic curvature is given by
Show that in the special case of constant , i.e. , this formula agrees with the equation
obtained earlier.