11.1Preliminary remarks
At the center of this Chapter is the celebrated divergence theorem, also known as Gauss's
theorem, as well as by a number of other names, which is a direct consequence of the
Fundamental Theorem of Calculus and, in some ways, a generalization of it.
The Fundamental Theorem of Calculus reads  (11.2) Specifically, the divergence theorem
reads
(11.2) Specifically, the divergence theorem
reads  (11.4) Note that the divergence theorem remains valid for tensors
with
vector elements, i.e.
(11.4) Note that the divergence theorem remains valid for tensors
with
vector elements, i.e.
where is the derivative of . In words, the Fundamental
Theorem of Calculus states that an integral of the derivative of a function can be expressed in terms of the
values of at the ends of the integration
interval. The divergence theorem applies to a multi-dimensional domain with boundary and states that the integral of the
divergence of a
tensor field over
the domain can be expressed in terms of the values of on
the boundary.
 (11.2)
(11.2) where are
the components the outward normal .
 (11.4)
(11.4) in which case both integrals
represent vector quantities.
Remarkably, the tensor formulation of the divergence theorem remains completely intact for curved
domains. Suppose that is a curved domain with a contour
boundary and let
be the surface components of its outward geodesic normal .  (11.6) Then, for a surface tensor ,
the divergence theorem reads
(11.6) Then, for a surface tensor ,
the divergence theorem reads
 (11.6)
(11.6) The curved form of the divergence
theorem also remains valid for tensors with vector elements, i.e.
Note that one of the essential
aspects of the divergence theorem is its invariant nature. Indeed, all elements of the theorem are
invariant objects that can, at least conceptually, be evaluated without the use of a coordinate
system.
Crucially, the scalar forms of the divergence theorem do not include any elements specific to
Euclidean spaces. Thus, the statements of the theorem remain meaningful -- and, perhaps more
importantly, correct -- in the more general Riemannian spaces and generalize to arbitrary
dimension. Note that while the use of the letters and , which we have typically used for two-dimensional domains
and their one-dimensional contour boundaries, suggests that the equation
is two-dimensional, it can actually
be validly interpreted for a domain of any dimension with an -dimensional boundary . In this arbitrary-dimensional Riemannian interpretation,
there is in fact no difference between the above form and
which can be considered a special
case of the more general Riemannian interpretation.
In the upcoming investigations, we will strike a compromise between the Euclidean and Riemannian
perspectives. For the sake of geometric intuition, we will discuss the specific case of a curved
two-dimensional surface in a Euclidean space. However, we
will restrict ourselves to analytical arguments that remain valid in the more general Riemannian
spaces.
11.2Several applications of the divergence theorem
Before we turn our attention to the derivation of the divergence theorem, let us take a look at a
few of its striking theoretical applications in a Euclidean space
11.2.1The integral
For any Euclidean domain , the integral of the unit normal over its boundary vanishes, i.e.
The demonstration of this
relationship by the divergence theorem is entirely straightforward. Since the integral in question
can be written in component form as
an application of the divergence
theorem yields
Now, thanks to the metrinilic
property of the covariant derivative with respect to the covariant basis , i.e.
we find that
as we set out to show. Finally, we note that this integral may be interpreted as the net force on
the body occupying the domain from a uniform pressure field. The fact that the
integral vanishes is consistent with our experience that a free body placed in a uniform pressure
field remains at equilibrium.
11.2.2The integral
For an application of the divergence theorem to a curved domain, let us now consider a similar
integral
of the curvature normal over
a surface patch with boundary . Under the Laplace model of capillary forces, this
integral may be interpreted as the net force of surface tension acting upon a soap film represented
by the curved surface . Since, in our experience, the center
of mass of a soap bubble does not experience acceleration under the influence of surface tension,
we expect this integral to also equal zero for a closed surface .
Recall that the combination
equals the surface Laplacian of the position vector , i.e.
or, equivalently, the divergence of
the surface contravariant basis ,
i.e.
Therefore, by the divergence
theorem, we have
Since the combination
represents the outward geodesic normal , we have
In words, the integral of the
curvature normal over
a surface patch equals the integral of the outward geodesic normal over the contour of the patch.
By all accounts, this relationship makes intuitive geometric sense, especially over a small patch:
the more curved is the patch, the more the geodesic normals at its boundary point in a consistent
direction. 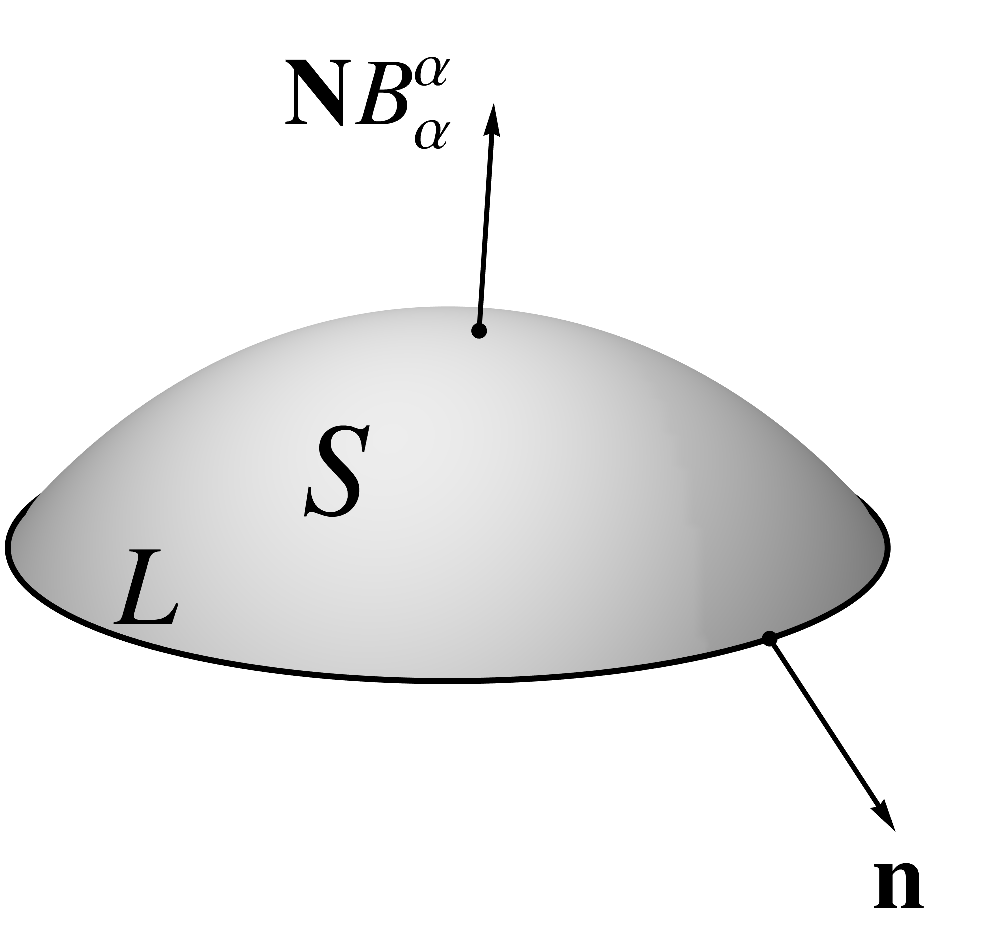 (11.18) If the patch is flat, i.e. , then the contour integral vanishes, i.e.
(11.18) If the patch is flat, i.e. , then the contour integral vanishes, i.e.
 (11.18)
(11.18) which is precisely the
two-dimensional version of the Euclidean formula
in the previous example.
Furthermore, we observe that the curvature normal at a
given point is given by the limit
where each integral is calculated
over a patch that is shrinking to the point in a regular manner. Dotting both
sides with gives an explicit limit for the mean curvature , i.e.
Finally, note that when the patch represents a closed surface, i.e.
there is no boundary, the formula
implies that the integral of the
curvature normal
vanishes, i.e.
as we expected.
11.2.3A few other surface integrals
The relationships discussed above have interesting "companion" formulas where the integrand is dot
multiplied by the position vector field . All of these formulas also follow from the divergence
theorem and their proofs are left as exercises.
For a closed surface , the volume of the enclosed domain is given in terms of the surface integral of by the formula
where is the dimension of the ambient space.
Similarly, the surface integral of over
yields its area according to the formula
For a non-closed patch with boundary , the analogous formula reads
(Note that despite the use of the
same letter, there is no relation between the dimension of the ambient space and the geodesic normal .)
What happens when the mean curvature in
the above integrals is replaced with Gaussian curvature ? It turns out that for a closed
two-dimensional surface , the integral of vanishes,
i.e.
Meanwhile, the companion formula
reads
11.3Arithmetic integrals
11.3.1Conversion of geometric integrals to arithmetic integrals
In Chapter TBD of Introduction Tensor Calculus we described the concept of a geometric
integral. Whether it is a volume integral
a surface integral
or a line integral
a geometric integral represents the
additive total of an invariant quantity over a geometric domain. In the same Chapter, we described
the evaluation of geometric integrals by a limiting procedure that involves subdividing the domain
into ever small pieces and adding up the individual infinitesimal contributions. The main takeaway
of the procedure is that, at least theoretically, geometric integrals can be evaluated by invariant
means without a reference to a coordinate system.
On the other hand, for many practical as well as theoretical reasons, geometric integrals must be
converted into arithmetic integrals which can be evaluated by the techniques of ordinary Calculus,
such as the Fundamental Theorem of Calculus, or other means, such as numerical computation.
Naturally, translation to an arithmetic integral becomes possible once the domain is referred to a
coordinate system. As we stated in Chapter TBD of Introduction to Tensor Calculus, the
volume integral
corresponds to the arithmetic
integral
where
is the volume element, the limits of integration reflect the domain, and it is further stipulated
that each lower limit is less than the corresponding limit, i.e.
Correspondingly, for surface and
line integrals, we have
and
with the same stipulation regarding
the integration limits. In order for these conversions to be valid, however, it must be
demonstrated that the arithmetic integrals are invariant with respect to coordinate changes. This
will be one of the tasks accomplished in the next Section.
For an example of conversion from a geometric to an arithmetic integral, consider the classical
calculation of the volume of a sphere of radius . As a geometric integral, is given by the formula
In Cartesian coordinates , the volume element
is given by
and therefore the corresponding
arithmetic integral reads
In spherical coordinates , on the other hand, the expression for the volume element
is
and therefore the corresponding
arithmetic integral reads
Both integrals evaluate to
consistent with the expected
invariance of the arithmetic integral with respect to coordinate changes. The latter integral,
however, is much easier to evaluate which illustrates the benefit of choosing a coordinate system
that is suited to a specific task.
11.3.2Invariance of arithmetic integrals under a change of coordinates
The argument presented in this Section relies on the change-of-variables theorem from Multivariable
Calculus. Our goal is to show that the two arithmetic integrals
and
constructed according to the
algorithm described above for two alternative coordinate systems and
,
are equal.
Recall that according to the change-of-variables theorem, the integral
for a function in coordinates can
be transformed to an equivalent integral in coordinates
by implementing three changes: 1. substituting the change of variables for the variables in the
function , 2. introducing a factor of , where is the matrix representing the
Jacobian ,
and 3. appropriately adjusting the limits of integration. These three steps are summarized by the
formula
When we apply this formula to the integral
we find
Of course, the composition is precisely , i.e. the field as a function of the primed
coordinates .
Also, recall from Section TBD of Introduction to Tensor Calculus that the volume element
transforms as a relative invariant of weight , i.e.
Thus, the combination
equals
and we have
as we set out to show.
11.4A demonstration of the divergence theorem in the arithmetic space
We will prove the divergence theorem in two steps. In this Section, we will demonstrate the
"arithmetic" version of the divergence theorem
for a tensor field
over a planar domain with boundary
referred to
Cartesian coordinates and . Although the domain and its
boundary need not be
the arithmetic representation of some curved domain with boundary , we chose to use the bar accent to highlight the
Cartesian nature of the present discussion. Note that
and
Therefore, in the unpacked form, the
arithmetic divergence theorem reads
Once we prove the arithmetic version of the divergence theorem, we will prove the general
divergence theorem
by reducing it to its arithmetic
version
11.4.1The arithmetic space
In Chapter TBD of Introduction to Tensor Calculus, we defined the arithmetic space
associated with a Riemannian space as a Cartesian visualization of the coordinate system in a
Euclidean space. For instance, for a two-dimensional surface referred to surface coordinates ,
the arithmetic space imagines the coordinates and
as
Cartesian coordinates in the plane.
For a specific example, consider a sphere of radius referred to the standard spherical
coordinates and . The corresponding arithmetic space occupies a rectangle in the plane,
as illustrated in the following figure. 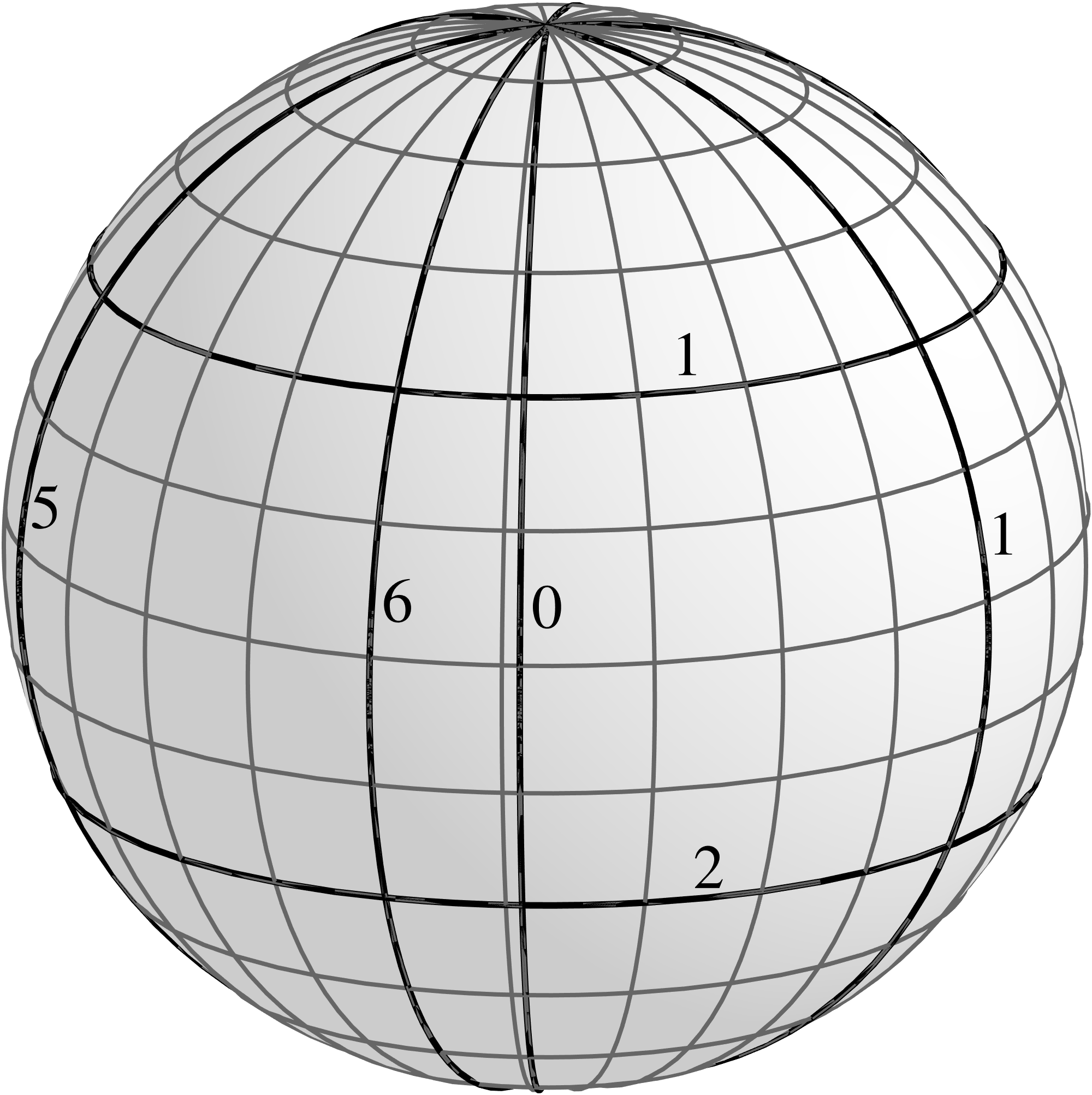
 (11.54) Furthermore,
to any surface curve described by the equations
(11.54) Furthermore,
to any surface curve described by the equations 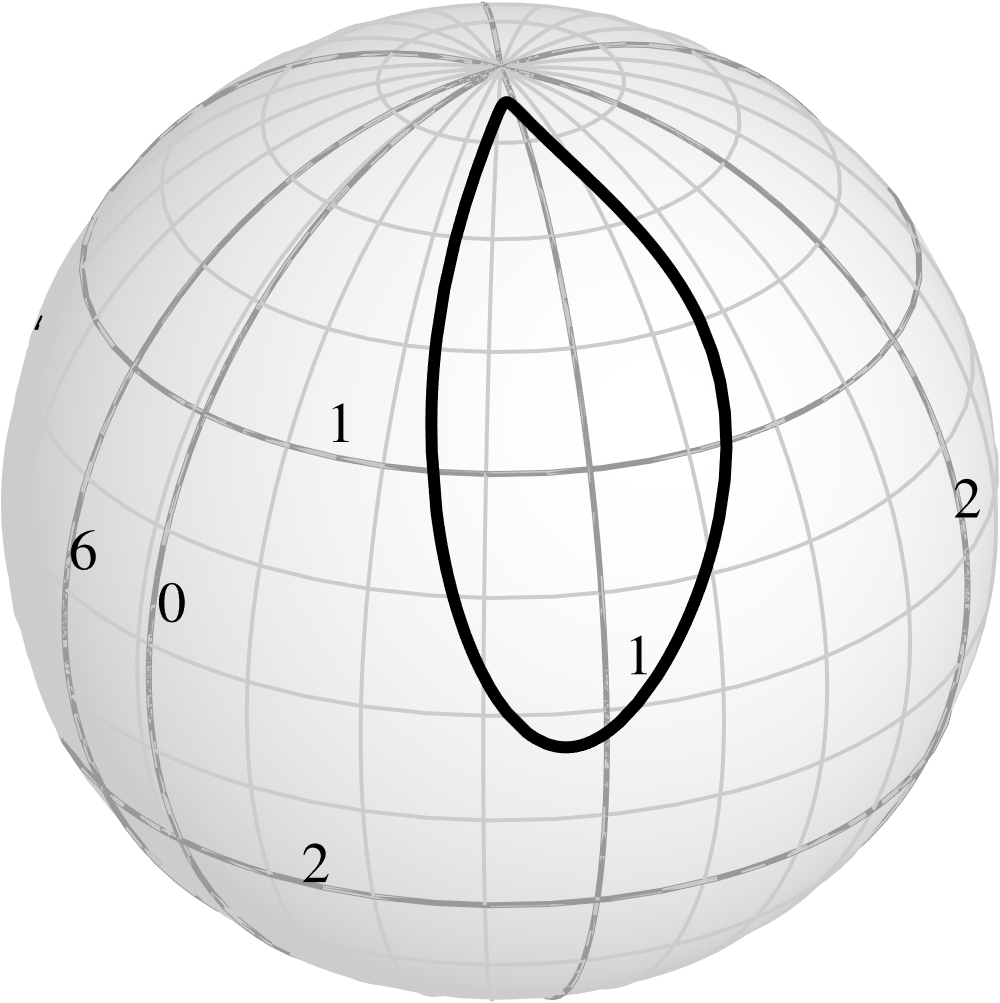
 (11.56) Entirely unsurprisingly, the two
shapes are completely different.
(11.56) Entirely unsurprisingly, the two
shapes are completely different.

 (11.54)
(11.54) there corresponds a curve in the
arithmetic space described by the same equations. The following figure shows an example of a
curve on a sphere along with its arithmetic counterpart.

 (11.56)
(11.56)In the upcoming demonstration of the divergence theorem, we will use a generic curved patch
illustrated in the following figure along with its arithmetic representation. 
 (11.57)
(11.57)

 (11.57)
(11.57)The fascinating aspect of the argument that we are about to present is that the geometry of
the arithmetic representation will take on central relevance. We will use the bar accent above the
symbol to denote the geometric objects in the arithmetic space. Thus, the domain corresponds to the arithmetic domain
and its
boundary corresponds to the curve . The shape of
the curve in the
arithmetic space will give rise to the normal field . And although we
are about to show that the components
and
are related, there is no reason whatsoever to expect that .
While the curves and live in
completely different spaces, they are, by construction, described by the same equations
Therefore, their respective shift
tensors
are identical as well.
On the other hand, the area elements
and
are different, as are the line elements
and .
Note that since the coordinates and
play
the role of Cartesian coordinates in arithmetic space, we have
We are now in a position to relate the components
of the geodesic normal to the original curve and the components
of the normal to the arithmetic
curve . Recall that
these components are given by the equations
and
where we once again point out that
the shift tensor is
the same for both curves. Expressing the Levi-Civita symbols in terms of the corresponding
permutation systems
and , we
find
Thus,
and therefore
Finally, since we
arrive at the formula
which will be used below to bridge
the divergence theorem to its arithmetic analogue.
11.4.2Useful extensions of the Fundamental Theorem of Calculus
The Fundamental Theorem of Calculus tells us that the operations of integration and differentiation
are the inverses of each other. The equation
can be seen as the "integral of the
derivative" form of the theorem. To obtain the "derivative of the integral form", allow the upper
limit of the integral to vary, i.e.
and differentiate both sides with
respect to , i.e.
It is this "derivative of the
integral" form, along with its straightforward extensions we are about to describe, that will be of
greater to use to us in our current discussion.
First, allow the upper limit to be a general function of . Then, by the chain rule, we have
It is left as an exercise to show
that the corresponding formula for a variable lower limit reads
Finally, suppose that the variable
also appears as a parameter in the integrand, i.e.
Then the integral is once again a
function of and can therefore be differentiated with respect to . Since an integral is essentially a sum, it is not
surprising that in order to differentiate the integral we must differentiate the integrand, i.e.
In summary, let us combine the three possible ways in which the integral can depend on the variable
in a single equation, i.e.
11.4.3The fundamental elements of planar curves given by explicit equations
Finally, our proof of the arithmetic divergence theorem will require expressions for the length
element and the normal components for a
curve given by an explicit function
in Cartesian coordinates. Recall the
equations from Chapter 4
where we switched from to and from to
to fit the current context. Note that the components of
were chosen so that they correspond to the "upward" normal.
Given the expression for , the line
integral
in arithmetic form reads
11.4.4The demonstration
Our argument will be limited to two-dimensional domains that correspond to a region between two
functions and , as illustrated in the following
figure.  (11.80) Note that along the top potion of the
curve, the exterior normal points up, while along the bottom portion of the curve, the exterior
normal points down.
(11.80) Note that along the top potion of the
curve, the exterior normal points up, while along the bottom portion of the curve, the exterior
normal points down.  (11.81) In the previous Section, we gave an expression for the
"upward" normal. However, on the bottom portion of the curve described by , the outward normal points
downwards and we must therefore adjust our expressions. We have
(11.81) In the previous Section, we gave an expression for the
"upward" normal. However, on the bottom portion of the curve described by , the outward normal points
downwards and we must therefore adjust our expressions. We have
 (11.80)
(11.80) (11.81)
(11.81)Denote the elements of the tensor field
by and , i.e.
Then the divergence
of
is given by
and the volume integral of
is given by the repeated integral
Breaking the repeated integral on
the right up into two, we have
We will now analyze each repeated integral individually. However, for both integrals, the key step
involves an application of the Fundamental Theorem of Calculus to the "inner" integral, i.e.  (11.89) As a result, the "outer" integrals
represent sums of combinations involving the boundary values of and as well as the derivatives of and and thus can
eventually be converted into line integrals over the boundary . This shows
how the Fundamental Theorem of Calculus reduces a domain integral to a boundary integral and
demonstrates why the divergence theorem may be considered a direct consequence of the Fundamental
Theorem of Calculus.
(11.89) As a result, the "outer" integrals
represent sums of combinations involving the boundary values of and as well as the derivatives of and and thus can
eventually be converted into line integrals over the boundary . This shows
how the Fundamental Theorem of Calculus reduces a domain integral to a boundary integral and
demonstrates why the divergence theorem may be considered a direct consequence of the Fundamental
Theorem of Calculus.
in the case of and
in the case of . For
each fixed value of , the integration in the inner integrals takes place along
the vertical interval from to and reduces the integral to the
difference of two values corresponding to the two ends of the integration intervals.
 (11.89)
(11.89)11.4.5Analysis of
We begin with the integral
Consider the inner integral
and notice that this integral can be
related to
with the help of the extension of
the Fundamental Theorem of Calculus derived earlier and captured by the equation
Substituting for , we find
Thus,
Now, recall that
and note that, by the Fundamental
Theorem of Calculus,
and each integral on the right vanishes since
and therefore the lower and the
upper limits for each integral coincide.
Consequently, the final expression for reads
We will now turn our attention to
the integral .
11.4.6Analysis of
The analysis of
is far simpler than that of since
the inner integral
is tailor-made for an application of
the Fundamental Theorem of Calculus. Indeed,
Therefore,
11.4.7Combining and
Combining the two integrals and grouping together the terms involving and those involving , we find
We can rewrite the integrand of each integral as a dot product, i.e.
Note the objects
are not quite the components
of the normal along and
, since
they are missing factors of
Similarly, the two integrals above
do not quite represent line integrals over and
since
they are missing the requisite factors of
Clearly, the missing factors are the
reciprocals of each other and therefore both problems can be easily remedied at the same time by
writing the integrals in the form
We now readily recognize the first integrand as and the second
integral as . Thus,
as we set out to prove.
11.5A demonstration of the divergence theorem
We will now use the "arithmetic" divergence theorem to prove the general formulation
for a curved domain with boundary .
As step one, convert the volume integral to a repeated arithmetic integral, i.e.
Note that we have omitted the limits
of integration for the repeated integrals and it is understood that the limits are chosen in such a
way as to correctly describe the domain .
Recall that, according to the Voss-Weyl formula
Thus the combination
is given by
and therefore
Notice that the integral on the
right equals the integral
since the "missing" factor of
equals . Thus, by the arithmetic divergence theorem that we have
just demonstrated, we have
Let us now express the line integral on the right by the corresponding arithmetic integral, i.e.
Recall that
Thus
which, of course, is the precisely
arithmetic representation for the line integral
In other words,
as we set out to show.
11.6Stokes' theorem
In order to demonstrate Stokes' theorem, introduce the unit tangent vector . Its ambient components are
given by expression
The contour integral is given by
where the integral on the right is
immediately subject to Gauss's theorem:
Expand the integrand by the product
rule
and apply the proper differential
identity to each term
The second and the third terms
vanish due to the skew-symmetry of the Levi-Civita symbol .
Thus, we are left with a single term
By the projection formula, we have
The term with the three normals
vanishes due to the skew-symmetry of
and the remaining term (with the indices rotated ) gives us precisely the statement of Stokes theorem
11.7Exercises
Exercise 11.1Show that the volume of the domain inside a closed surface is given by the equation
where is the position vector, is the outward normal and is the dimension of the ambient space.
Exercise 11.2Show that the area of a closed surface is given by the equation
where is the position vector, is the outward normal, and is the dimension of the ambient space.
Exercise 11.3Show that the area of a non-closed surface with boundary is given by the equation
where is the position vector, is the outward normal, is the outward geodesic normal, and is the dimension of the ambient space.
Problem 11.1Show that for a two-dimensional closed surface ,
where is the Gaussian curvature.
Problem 11.2Show that for a two-dimensional closed surface ,
Exercise 11.4Show that the vector whose components are given by
is indeed the unit tangent to the contour boundary. That is, is unit length
orthogonal to the surface normal
and the contour normal
Exercise 11.5Explain why the term in the proof of Stokes' theorem vanishes.