To my generous Patreon editors: please note that this Chapter is not quite ready to be edited. As
it often happens, the introductory chapter will be the last one to be completed before the book is
done!
This is a continuation of An Introduction to Tensor Calculus which was devoted to the
construction of the analytical framework of Tensor Calculus. In this book, we will use the Tensor
Calculus framework to study shape -- in other words, curvature.
Historically, the development of understanding of curvature unfolded in two distinct phases. The
first phase, which lasted until about the middle of the nineteenth century, was preoccupied with
gaining insight into curvature by developing measures for quantifying it and discovering
fundamental laws relating those measures. This phase is associated primarily with the
groundbreaking works of Leonhard Euler and Carl Friedrich Gauss. The second phase, originated by
Gauss and advanced by Bernhard Riemann and Albert Einstein, is aimed at understanding the geometric
properties of the underlying space itself.
Our narrative will speak to both of these elements, but it will have a different focal point. Our
focus will be on the development of the analytical framework for studying curvature.
1.1Curvature and Tensor Calculus
Although spectacular in terms of achievement, development of humanity's understanding of curvature
has been laborious and slow. Meanwhile, the tensor framework will make most of the concepts and
equations appear deceptively simple as many of the most profound and hard-fought facts will fall
before us like dominos. For example, Gauss's famous Theorema Egregium -- the Remarkable
Theorem -- will come across as almost entirely self-evident. His celebrated equations of the
surface
will be derived in an exercise in the next Chapter. Meanwhile, Euler's remarkable discovery
that the surface swept out by tangents to a three-dimensional curve is developable will, too, be
found in an exercise. In fact, most of the facts that might occur to us naturally, some found in
exercises, would have constituted results worthy of an admirable nineteenth-century doctoral
thesis.
Such retrospective ease is not unique to Tensor Calculus but is a general phenomenon of human
forward movement. In music, it is said, the dissonance of today is the consonance of
tomorrow. This law of evolution of human thought should in no way diminish our admiration for
the remarkable achievements of the great minds of the past. As we celebrate our superior tools of
the trade, we should contemplate what has been lost because of them.
1.2The three degrees of curvature
Let us begin by having an informal discussion of curvature and, in particular, its interplay with
coordinates systems. The crucial observations made in this Section, although stated as facts, are
meant to appeal to your geometric intuition and to guide our future analytical
investigations.
1.2.1Curvilinear coordinates in a Euclidean space
In Introduction to Tensor Calculus, we devoted much of our attention to Euclidean spaces
characterized by straightness. A Euclidean space can accommodate a straight line in any direction
and can therefore be referred to an affine -- and, in particular, Cartesian -- coordinate system.
Nevertheless, in almost all of our theoretical explorations we assumed a more general curvilinear
coordinate system.  (1.1) Our primary motivation for this choice
was to eliminate the possible artifacts of a special coordinate system. Thus, we did not assume
that the chosen coordinate system had any special features, such as straight regularly-spaced
coordinate lines. When we did, on rare occasions, resort to affine coordinates, it was to
specifically call attention to the Euclidean nature of our space. Our diligent self-limitation paid
off as it led us to develop a more general framework of great robustness.
(1.1) Our primary motivation for this choice
was to eliminate the possible artifacts of a special coordinate system. Thus, we did not assume
that the chosen coordinate system had any special features, such as straight regularly-spaced
coordinate lines. When we did, on rare occasions, resort to affine coordinates, it was to
specifically call attention to the Euclidean nature of our space. Our diligent self-limitation paid
off as it led us to develop a more general framework of great robustness.
 (1.1)
(1.1)However, in order to arrive at such a framework, we had to first contend the curvature effects
associated with curvilinear coordinates. The most obvious and striking complication lies in the
fact that the covariant basis , which
is regular (i.e. constant) in affine coordinates, varies from one point to the next in curvilinear
coordinates.  (1.2) As a result, vectors at different
points cannot be compared, added, or otherwise related in any way by analyzing their components in
the familiar Cartesian fashion. Furthermore, the partial derivative
(1.2) As a result, vectors at different
points cannot be compared, added, or otherwise related in any way by analyzing their components in
the familiar Cartesian fashion. Furthermore, the partial derivative
 (1.2)
(1.2) applied to the components of a
vector field does not fully capture its rate of change since it ignores the variability in the
accompanying basis. This loss of geometric information manifested itself in the lack of the tensor
property of the partial derivative of a tensor.
Outside of our geometric study of curves, this was our first encounter with the effects of
curvature. However, this curvature is of the spurious nature: since a Euclidean space is
fundamentally straight, these effects are artifacts of our analysis and, as a result, can be
completely mitigated. This is accomplished by introducing the covariant derivative . The
covariant derivative restores the tensor property, possesses the metrinilic property with respect
to the basis, i.e.
which is akin to the affine property
and preserves the product rule.
In summary, the tensor framework handles this lowest "degree" of curvature rather easily while
offering a great deal of insight.
1.2.2Developable surfaces
The next "degree" of curvature is represented by surfaces that can be formed by smoothly curving a
flat sheet of paper, i.e. a region of a plane, without any distortion. For a transformation to not
introduce any distortion it must preserve the distance between any two points as measured within
the surface. We must note, however, that the concept of distance as measured within the
surface is arguably unclear and needs to be precisely defined. Nevertheless, such
transformations are known as isometric and surfaces that can be isometrically transformed
into a region of a plane are known as developable. Thus, we can continue to think of a
developable surface as a Euclidean plane from the viewpoint of their internal geometry but not from
the overall three-dimensional point of view.  (1.6)
(1.6)
 (1.6)
(1.6)Developable surfaces were first investigated by Euler in his 1772 work De solidis quorum
superficiem in planum explicare licet or On shapes that can be unwrapped onto a plane.
The classical examples of developable surfaces are the cylinder and the cone. 
 (1.7) Note that these two surfaces need
to be cut in order to be transformed into a region of a plane.
(1.7) Note that these two surfaces need
to be cut in order to be transformed into a region of a plane.

 (1.7)
(1.7)Another general type of a developable surface is known as the tangent developable of a
curve. It is the surface swept out by the tangent lines to a three-dimensional curve.  (1.8) In De solidis quorum superficiem in planum explicare
licet, Euler not only demonstrated that the tangent developable is, indeed, a developable
surface, but that every developable surface that is not a cylinder or a cone is a tangent
developable for some curve.
(1.8) In De solidis quorum superficiem in planum explicare
licet, Euler not only demonstrated that the tangent developable is, indeed, a developable
surface, but that every developable surface that is not a cylinder or a cone is a tangent
developable for some curve.
 (1.8)
(1.8)On the one hand, developable surfaces are undeniably curved. On the other hand, they allow regular
coordinate systems which can be accomplished easily by referring the flat sheet of paper to a
regular coordinate system prior to curving it into the final shape, as illustrated in the following
figure. 
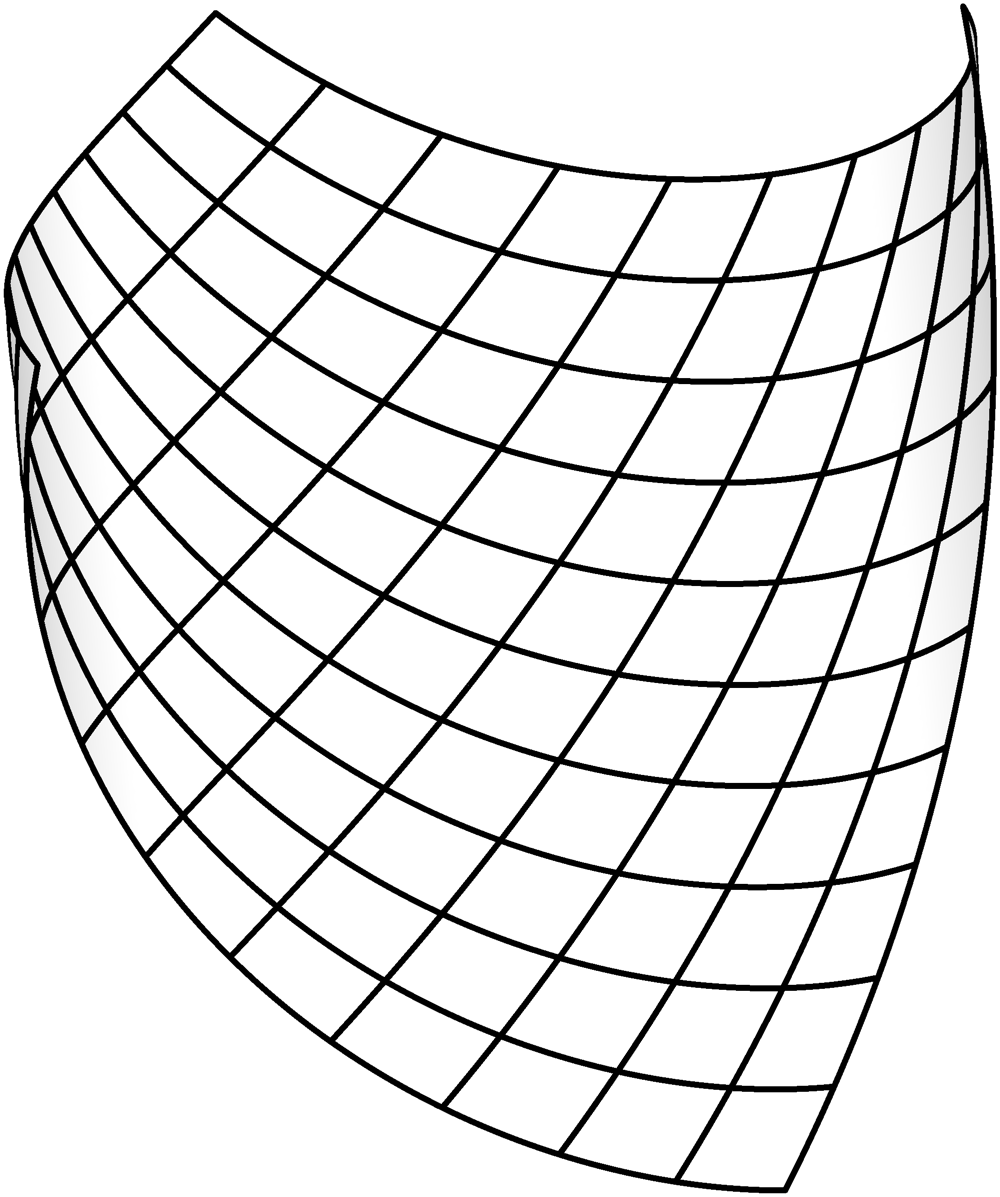 (1.9) Of course, we must clarify the sense in which a coordinate
system on the curve surface is regular. Indeed, in the above figure, all of the coordinate
lines are curved and the coordinate nodes are not arranged in any kind of regular pattern in the
three-dimensional space. Yet, it is intuitively clear that, with respect to the surface, the
coordinate lines are indeed regular. Thus, there is a clear dichotomy between how the image
appears in the overall three-dimensional space and how it is perceived within the surface. We will
use the term intrinsic to describe the geometric action that takes place strictly in the
surface without a reference to ambient objects. For example, we will describe developable surfaces
as curved in the three-dimensional sense and as flat in the intrinsic sense.
(1.9) Of course, we must clarify the sense in which a coordinate
system on the curve surface is regular. Indeed, in the above figure, all of the coordinate
lines are curved and the coordinate nodes are not arranged in any kind of regular pattern in the
three-dimensional space. Yet, it is intuitively clear that, with respect to the surface, the
coordinate lines are indeed regular. Thus, there is a clear dichotomy between how the image
appears in the overall three-dimensional space and how it is perceived within the surface. We will
use the term intrinsic to describe the geometric action that takes place strictly in the
surface without a reference to ambient objects. For example, we will describe developable surfaces
as curved in the three-dimensional sense and as flat in the intrinsic sense.

 (1.9)
(1.9)A surface swept by straight lines (which are not necessarily the tangents of a given curve) is
known as a ruled surface. We will show that every developable surface is ruled. This
becomes intuitively clear when inspecting a curved sheet of paper and noting that, at every point,
the direction in which the sheet is straight continues to infinity or, at least, to the edge of the
sheet.  (1.10) The shape of a fluttering flag is
often used as an example of a developable surface since a flag, it would seem, can be flattened out
without distortion. However, a fluttering flag is clearly not a ruled surface since it is not
developable, as seen in the following figure.
(1.10) The shape of a fluttering flag is
often used as an example of a developable surface since a flag, it would seem, can be flattened out
without distortion. However, a fluttering flag is clearly not a ruled surface since it is not
developable, as seen in the following figure.  (1.11)
Therefore, modeling it as a developable surface will inevitably fail to capture some of its
properties.
(1.11)
Therefore, modeling it as a developable surface will inevitably fail to capture some of its
properties.
 (1.10)
(1.10) (1.11)
(1.11)Finally, note that not all ruled surfaces are developable as evidenced by the parabolic hyperboloid
in the following figure.  (1.12)
(1.12)
 (1.12)
(1.12)In our pursuit of understanding curvature, one of our overarching goals will be to derive
analytical criteria for developable surfaces.
1.2.3Intrinsically curved surfaces
Non-developable surfaces represent the third, highest "degree" of curvature. Such surfaces can be
considered to be curved in a more profound way since they cannot be flattened without distortion.
For example, a sphere -- or any part, no matter how small, thereof -- cannot be unwrapped onto a
region of a plane without distortion. This is a well-known phenomenon in cartography when one
attempts to represent the round Earth on a two dimensional map. When one attempts to do so in a
smooth fashion, significant distortion results. 
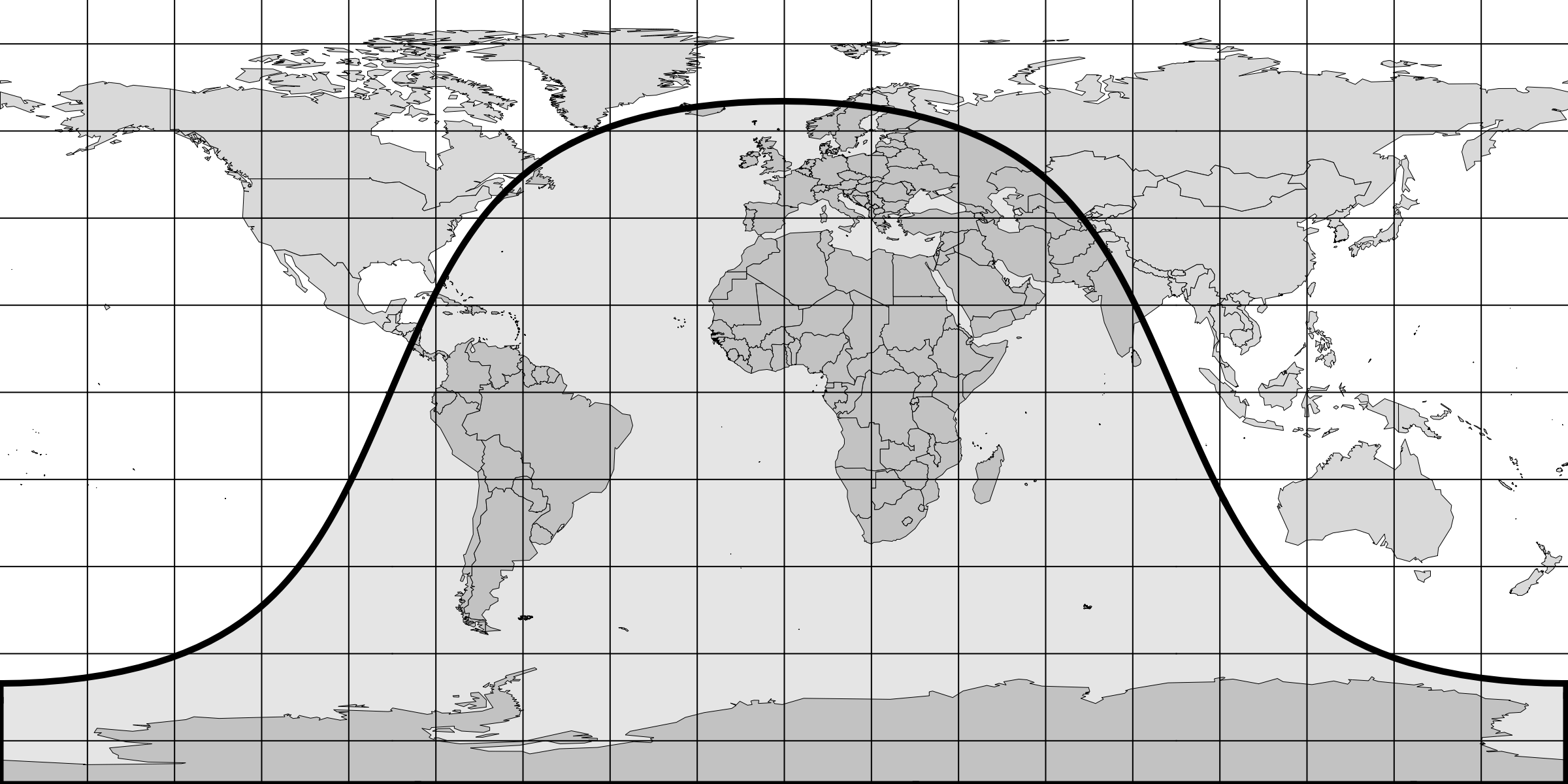 (1.13) The amount of
distortion can be reduced with the help of tears, but it cannot be eliminated.
(1.13) The amount of
distortion can be reduced with the help of tears, but it cannot be eliminated.  (1.14)
(1.14)

 (1.13)
(1.13) (1.14)
(1.14)It follows from these observations that a non-developable surface does not admit an intrinsically
regular coordinate system. This has important implications since a number of arguments used in
Introduction to Tensor Calculus relied on the availability of affine coordinates. In
particular, the fact the Riemann-Christoffel tensor vanishes fundamentally relied on affine
coordinates. We can therefore expect that the corresponding surface object continues to vanish for
developable surfaces but not for non-developable surfaces. In fact, this holds the promise of
yielding a criterion for developable surfaces which will be explored in Chapter 7.
1.3A brief review of Euclidean spaces and the tensor framework
Let us now summarize the key concepts and notation introduced in Introduction to Tensor
Calculus.
The position vector at a point in a Euclidean space is the vector
that emanates from an arbitrary fixed point , known as the origin, and terminates
.
Refer the Euclidean space to arbitrary coordinates . Then
the position vector becomes a function of the coordinates which, in a
three-dimensional space reads
We typically abbreviate such
expressions by representing the enumerated arguments of functions by a single letter, i.e.
The covariant basis is
given by the partial derivative
The covariant metric tensor
is
obtained by pairwise dot products of the covariant basis vectors, i.e.
The contravariant metric
tensor
is the matrix inverse of ,
i.e.
where
is the Kronecker delta system. The contravariant basis is
given by the contraction
The covariant and the contravariant
bases are mutually orthogonal, i.e.
Also, the last property can serve as
an alternative definition of the contravariant basis . The
determinant of the covariant metric tensor is
denoted by and its square root, ,
is referred to as the volume element.
The permutation systems
and
have the following values
The Levi-Civita symbols
and
are defined by the identities
The complete delta system
is given by
or, equivalently,
and can be expressed in terms of the
Kronecker delta by the identity
The partial delta system has
the values
delta_{rs}^{ij}=left{ begin{tabular}
{ll} & & & end{tabular}
right. end{equation} It satisfies the identity
and can be obtained from the
complete delta system
by a single contraction, i.e.
Thus, we also have the frequently
used identity
1.3.1Index juggling
The metric tensors are used to implement the operations of index juggling. Contraction with
the covariant metric tensor is
captured by index lowering, e.g.
Contraction with the contravariant
metric tensor
is captured by index raising, e.g.
The two operations are the inverses
of each other.
1.3.2The Christoffel symbols
The Christoffel symbol
is given by
or, equivalently, by
The symbol
is sometimes referred to as the Christoffel symbol of the second kind. The Christoffel symbol of
the first kind is
obtained by lowering the index on ,
i.e.
Alternatively, is
given by
The partial derivative of the covariant metric tensor
with respect to
is given by the identity
The derivative of the volume element
is given by
The divergence of a
variant field is
given by the Voss-Weyl formula
Correspondingly, the Laplacian of a scalar field is given by
The Christoffel symbol vanishes in affine coordinates, i.e.
Its nonzero elements in cylindrical
coordinates are
while in spherical coordinates they are
1.3.3The covariant derivative
For a variant
with a representative collection of indices, the covariant derivative is
given by the identity
The cornerstone feature of the covariant derivative is its tensor property -- namely, that it
produces tensor outputs for tensor inputs. Furthermore, the covariant derivative satisfies the sum
rule, the product rule, commutes with contraction. It coincides with the partial derivative in
affine coordinates. Finally, it is metrinilic with respect to all of the fundamental tensors in a
Euclidean space, i.e.
and
Note that the metrinilic property
follows easily by a combination of the tensor property and the fact that the covariant derivative
coincides with the partial derivative in affine coordinates.
1.3.4The commutator and the Riemann-Christoffel tensor
Covariant derivatives commute. In other words, the commutator
vanishes for all inputs, i.e.
Since it can be generally shown that
for any , we
conclude that
The combination on the left is a tensor known as the Riemann-Christoffel tensor ,
i.e.
Thus the fact that covariant
derivatives commute is equivalent to the statement that the Riemann-Christoffel tensor vanishes,
i.e.
Note that the logic that leads to this conclusion that covariant derivatives commute (and therefore
) fundamentally relies on the Euclidean nature of the
space. The argument goes like this. A Euclidean space admits an affine coordinate system where the
covariant derivative coincides with the partial derivative, thus
Meanwhile, as we know from ordinary
Calculus, partial derivatives commute, i.e.
Therefore, in affine coordinates,
the commutator
vanishes, i.e.
However, since
is a tensor, it must vanish in all coordinate systems which completes the argument.
Note, that we can expect the same argument to work for developable surfaces since they admit
regular affine-like coordinate systems.
Conclusion to follow.