In the preceding Chapter, we introduced some of the most fundamental objects in the analysis of
surfaces without the help of coordinates in the ambient space. Perhaps the highlight of that
Chapter was the emergence of the curvature tensor in
the equation
and its appearance in the Gauss
equations
which was demonstrated in the exercises. All of that was accomplished without ambient coordinates.
On the other hand, consistent with our experience with Euclidean spaces, our theoretical findings
cannot be used to calculate any characteristics, including curvature, of any concrete surface due
to the limited computational capabilities of geometric objects.
In this Chapter, we will remedy that shortcoming by introducing coordinates in the ambient space.
This development will compel us to study the interplay between two coordinate systems: the surface
coordinates
and the ambient coordinates . This
interplay will yield variants of a new kind -- those that feature both surface and ambient indices
-- which will invite us to extend the concept of a tensor to include two types of indices.
In this Chapter, our attention will be occupied by the shift tensor ,
which describes the tangent space, and the components of
the unit normal, which describe the orthogonal space -- and, of course, the interplay between the
two. The theory developed in this Chapter will be illustrated in the next Chapter with examples
involving some of the most common surfaces, such as the sphere, the cylinder, and the torus.
3.1The equations of a surface
Consider a two-dimensional surface embedded in a three-dimensional space and referred to surface
coordinates .
Furthermore, introduce an arbitrary coordinate system in
the ambient space.
With the help of the two coordinate systems, the surface can be described parametrically,
i.e. by specifying the values of the ambient coordinates as functions of surface coordinates. For a
two-dimensional surface in a three-dimensional space, a parametric specification requires three
functions of two variables. These functions are called the equations of the surface and are
denoted by the same symbols as
the ambient coordinates, i.e.
As usual, these equations can be captured by a single indicial identity,
which, by collapsing the function
arguments, can be written in an even more compact form
Not surprisingly, the one operation
that can be applied to the equation of the surface, i.e. differentiating with respect to
resulting in the system
will give rise to an important
object that will occupy much of our attention in the rest of our narrative.
Before proceeding with our analysis, however, let us consider a few classical examples of
two-dimensional surfaces and one-dimensional planar curves.
3.2Examples of two-dimensional surfaces
3.2.1A sphere of radius
Refer a sphere of radius to the surface spherical coordinates
described in the previous Chapter. 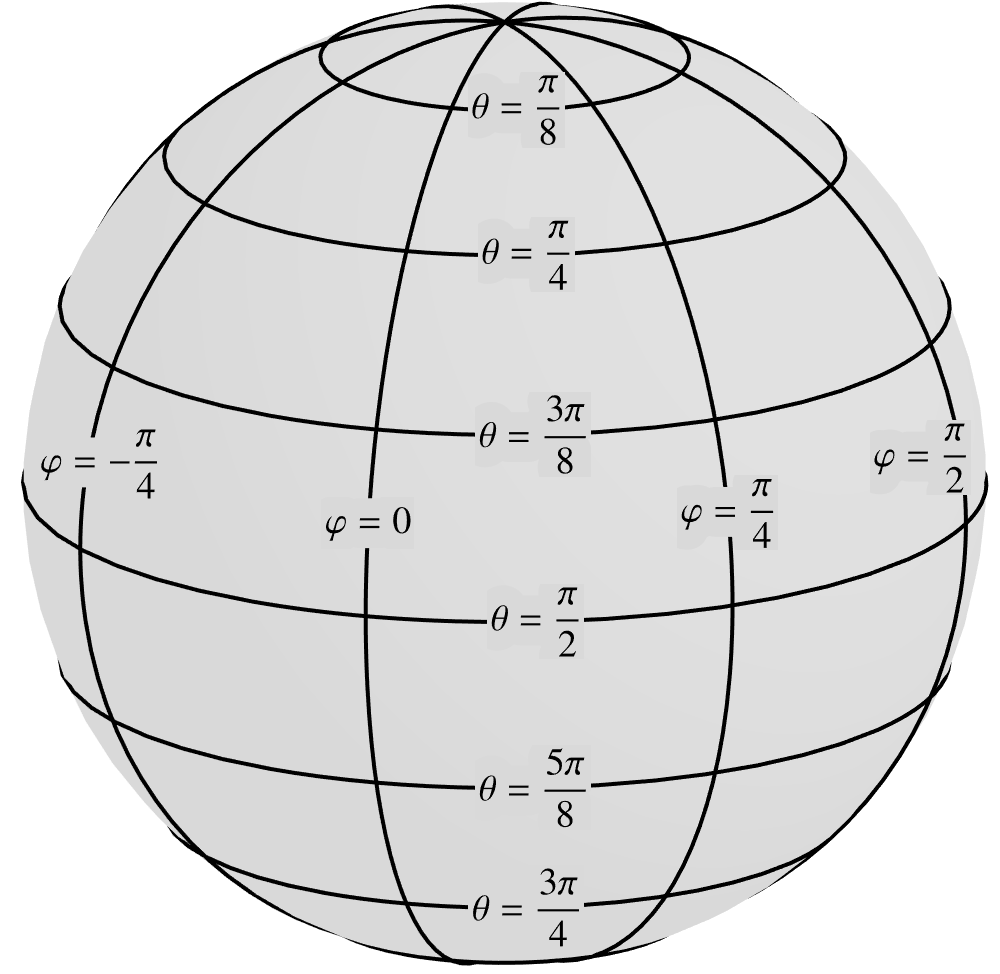 (3.7) If the ambient space is referred to
Cartesian coordinates , aligned with the surface coordinates
in the usual way, then the equations of the surface read
(3.7) If the ambient space is referred to
Cartesian coordinates , aligned with the surface coordinates
in the usual way, then the equations of the surface read
 (3.7)
(3.7)When the ambient space is referred to spherical coordinates , the
equations of the surface appear in a particularly simple form
The simplicity of these expressions indicates that spherical coordinates in the ambient space are a
natural choice for describing the surface of a sphere. This simple example also illustrates the
profound dependence of the equation of a surface on the choice of coordinates.
3.2.2A cylinder of radius
Refer a cylinder of radius to coordinates illustrated in the following figure.
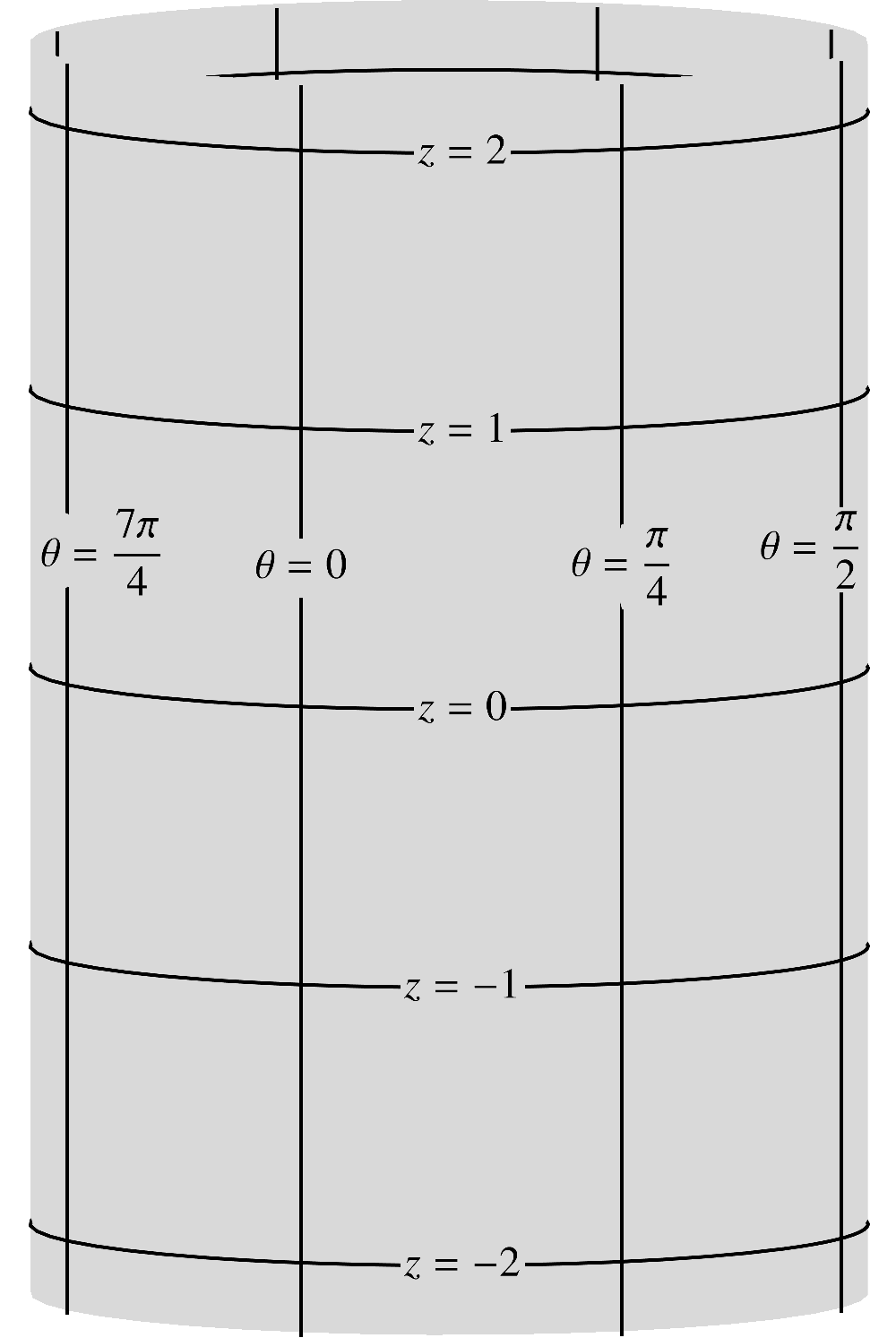 (3.14) If the ambient space is referred to
Cartesian coordinates , the
equations for the cylinder read
(3.14) If the ambient space is referred to
Cartesian coordinates , the
equations for the cylinder read
 (3.14)
(3.14)
If the ambient space is referred to cylindrical coordinates , the
equations become even simpler, i.e.
Interestingly, note that the equations of a sphere in spherical coordinates are the same as the
equations of a cylinder in cylindrical coordinates.
3.2.3A surface of revolution
A surface of revolution is formed by rotating a planar curve around a straight line (within the
same plane) known as the axis of rotation. The curve that is being rotated may be referred
to as the profile of the shape. Notice that both a sphere and a cylinder, as well as the
upcoming torus, are examples of shapes of revolution. 
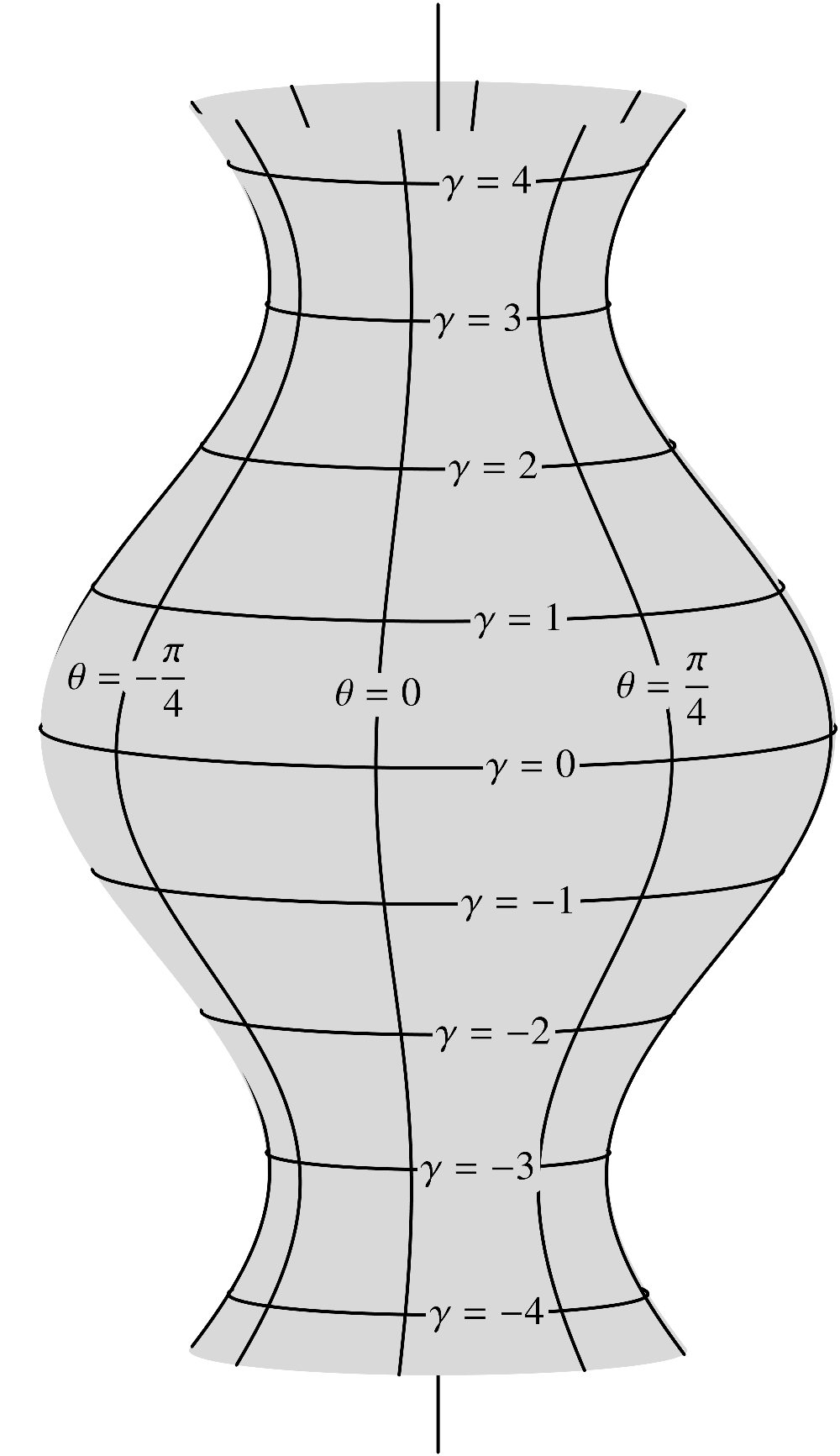 (3.21)
(3.21)

 (3.21)
(3.21)It is natural to choose the angle of rotation to be one of the two surface
coordinates. The other coordinate can be any parameter . If the ambient space is referred to
Cartesian coordinates, then the shape of revolution about the -axis is given by
where is the location of the point along the -axis and is the distance away from the -axis. If the ambient space is instead
referred to cylindrical coordinates , we
once again obtain equations of utmost simplicity, i.e.
where is the location of the point along the -axis and is the distance away from the -axis. Finally, note that it is very
common to choose
in which case corresponds exactly to the location
of the point along the axis of rotation.
3.2.4A torus with radii and
A torus is the shape of revolution of a circle of radius whose center is the distance from from the rotation axis.  (3.29) This simple profile corresponds to the functions
(3.29) This simple profile corresponds to the functions 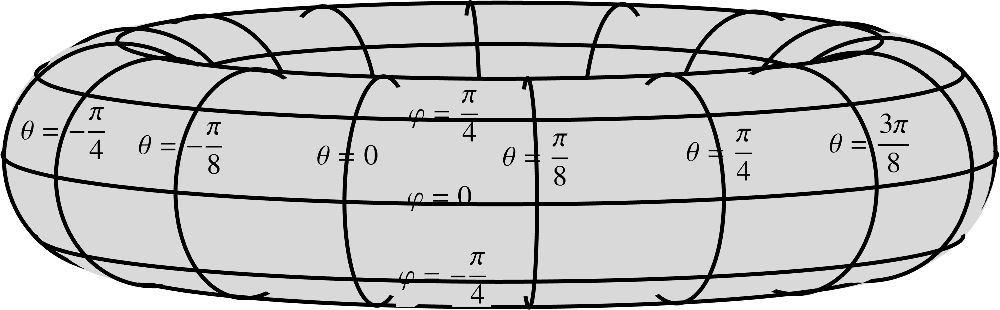 (3.32) Thus, the equations of the torus read
(3.32) Thus, the equations of the torus read
 (3.29)
(3.29)
where we decided to use the letter instead of because of its interpretation as an
angle.
 (3.32)
(3.32)
where both and vary from to .
3.3Examples of planar curves
A planar curve is a one-dimensional "surface" embedded in a two-dimensional Euclidean plane which
we will typically refer to either Cartesian or polar coordinates.
3.3.1Planar curves in Cartesian coordinates
The most common type of curve that we encounter in our introductory Calculus courses is the graph
of a function . For example, the curve
corresponding to the function  (3.37) Every curve that represents the graph of a function can also be represented
parametrically by the equations
(3.37) Every curve that represents the graph of a function can also be represented
parametrically by the equations
is shown in the following figure.
 (3.37)
(3.37)Of course, not every planar curve corresponds to the graph of a function. A quintessential curve
that is not the graph of a function is a circle. The following figure illustrates a circle of
radius centered at a point with coordinates
.  (3.40) It is described by the equations
(3.40) It is described by the equations
 (3.40)
(3.40)
where, once again, we used instead of because of its interpretation as an
angle.
For a more intricate example, consider the equations  (3.45)
(3.45)
that describe the curve in the following figure.
 (3.45)
(3.45)Interestingly, many curves that can be represented by a graph of a function are still more easily
represented parametrically. One example is a cycloid, which represents the trajectory of a point on
a wheel rolling without slippage along a straight line.  (3.46) A cycloid that corresponds to a wheel of radius is specified by the equations
(3.46) A cycloid that corresponds to a wheel of radius is specified by the equations
 (3.46)
(3.46)3.3.2Planar curves in polar coordinates
A general planar curve in polar coordinates is given by  (3.53) For another example, the curve given by the equations
(3.53) For another example, the curve given by the equations  (3.56)
(3.56)
As we described in Chapter TBD of Introduction to Tensor Calculus, can assume negative values and can assume any value whatsoever. When is negative, the point with coordinates is plotted as . To repeat an example from that Chapter, the
curve given by the equation
is shown in the following figure.
 (3.53)
(3.53)
has the following shape:
 (3.56)
(3.56)Polar coordinates have their own version of a graph, i.e. curves that may be described by
specifying as a function of  (3.61) It is also possible, but less common, to specify as a function of .
(3.61) It is also possible, but less common, to specify as a function of .
which is equivalent to the
parametric equations
For example, the following spiral corresponds to
where varies form to .
 (3.61)
(3.61)This wraps up the description of the most common surfaces and curves that will be used throughout
the rest of our narrative as illustration of the relevant concepts.
3.4The shift tensor
We now turn our attention to the shift tensor -- a
central object in the analysis of embedded surfaces that represents the tangent space. Furthermore,
the shift tensor helps relate corresponding surface and ambient quantities. In fact, we will
approach the shift tensor by exploring the relationship between the surface basis and
the ambient basis .
Recall that the ambient covariant basis is
given by the equation
where is the position vector as a function of the
ambient coordinates .
Similarly, the surface covariant basis is
given by the equation
where is the surface restriction of the position
vector as a function of the surface coordinates .
As usual, in order to relate the derivatives
we must first relate the functions
To find the correct relationship,
imagine the position vector corresponding to a specific surface point with surface coordinates .
The vector can be obtained in two alternative ways. The first is to
evaluate the function at the coordinates .
The second is to determine the ambient coordinates of
the point by evaluating the equations of the
surface at
and then to evaluate the function at the resulting values of the coordinates
. This
line of reasoning yields the identity
Differentiating this identity by the chain rule with respect to ,
we have
where we recognize two of the three
elements, i.e.
The third element,
is the shift tensor! It is
denoted by the symbol , i.e.
By convention, the Latin index is
considered first and the Greek index is considered second. Therefore, we do not need a placeholder
to help us track the order of the indices. Meanwhile, the precise meaning of the word
tensor, when applied to an object featuring both ambient and surface indices, will be
described in the next Section.
With the help of the symbol , the
relationship between the surface and the ambient bases reads
For each , this identity represents the vector
as a
linear combination of the ambient basis vectors . Thus,
are
the components of the surface basis element with
respect to the ambient basis . It is
for this reason that the shift tensor is said to represent the tangent space.
Recall that the ambient components of a
vector are given by the dot product
Therefore,
In other words, the elements of the
shift tensor are the pairwise dot products of the ambient and surface bases. By index juggling, we
easily obtain the equivalent identities
Although we will save the bulk of our discussion of specific surfaces until the next Chapter, let
us give the shift tensor for a sphere of radius in both Cartesian and spherical
ambient coordinates. As we stated earlier in this Chapter, for the ambient space is referred to
Cartesian coordinates , the equations of the sphere read
The shift tensor then
corresponds to the matrix
Meanwhile, for the ambient space referred to spherical coordinates , the
equations of the surface read
the shift tensor
corresponds to the matrix
Once again, the equation 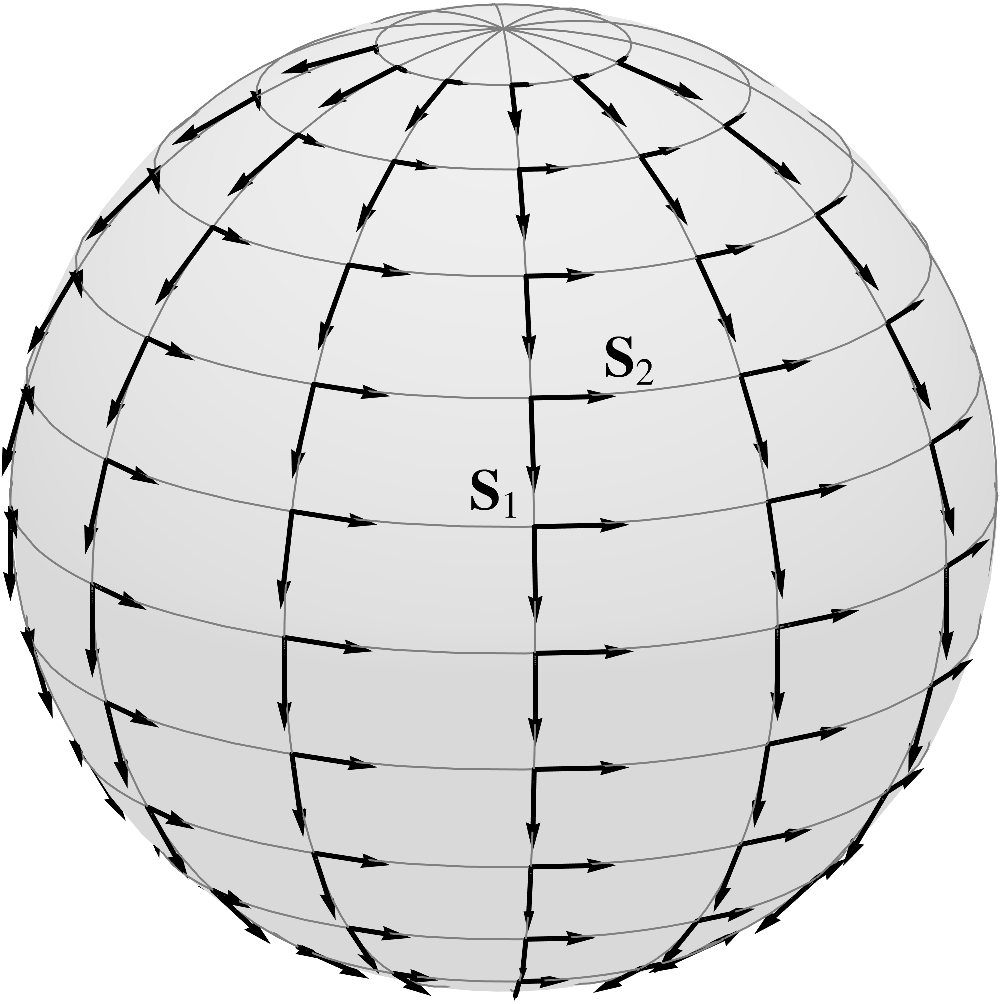 (3.76) In particular, when spherical coordinates are
chosen in the ambient space, the surface covariant basis is
represented by the last two vectors of the ambient basis , i.e.
(3.76) In particular, when spherical coordinates are
chosen in the ambient space, the surface covariant basis is
represented by the last two vectors of the ambient basis , i.e.
tells us that the elements of the
shift tensor are the components of the surface covariant basis with
respect to the ambient covariant basis . Thus,
the columns of each matrix representing the shift tensor are the ambient
components of the corresponding surface covariant basis vectors. For the surface coordinates , the covariant basis on the
sphere is shown in the following figure and you should confirm that the columns of the matrices
above correctly represent these vectors.
 (3.76)
(3.76)
which corroborates the particularly simple form of the shift tensor.
The shift tensor is
our first example of a variant featuring both ambient and surface indices. Therefore, we must
revisit the concept of a tensor as
forces us to contend with two simultaneous coordinate changes: one in the ambient space and one on
the surface. This is the task to which we will now turn our attention.
3.5Tensors with ambient and surface indices
From the identity
it is clear that the elements of the
shift tensor
change with both the ambient and surface coordinates. This invites us to expand the concept of a
tensor to include transformations under simultaneous changes of ambient and surface
coordinates. Before we give the general definition, let us examine how the shift tensor behaves in
those circumstances.
Let and
be the unprimed and primed ambient coordinates related by the functions
At the same time, let
and
be the unprimed and primed surface coordinates related by the functions
Also recall the definitions of the associated Jacobians, i.e.
and
In the primed coordinates, the shift tensor is
given by the equation
The ambient contravariant basis
depends only on the choice of the ambient coordinates and, being a tensor, transforms according to
the rule
Similarly, the surface covariant
basis
depends only on the choice of the surface coordinates and, being a tensor, transforms according to
the rule
Therefore, for the shift tensor
, we
have
In summary,
In words, the shift tensor
exhibits the properties of a tensor with respect to changes of both ambient and surface
coordinates.
Let us use this behavior as a blueprint for an expanded definition of a tensor. Consider a variant
with a representative collection of ambient and surface indices. Then
is an (absolute) tensor if its elements
in the primed coordinate systems are related to
by the equation
According to this definition, the
shift tensor is indeed a tensor. Furthermore, all previously defined surface and ambient variants
that are tensors in the original sense remain tensors in the sense of the new, more general
definition. Of course, for tensors in the ambient space, we must limit our attention to their
surface restrictions in order for the new definition to apply.
Finally, it is left as an exercise to demonstrate all of the common properties of tensors including
the sum, product, and contraction properties, as well as the quotient theorem.
3.6The ambient coordinates of a vector in the tangent plane
Consider a vector in the tangent plane at a point on the surface. Like all vectors in
the tangent plane, can be decomposed with respect to the surface covariant basis
,
leading to the contravariant components ,
i.e.
However, like any vector
whatsoever, whether it lies in the tangent plane or not, can also be decomposed with respect to the ambient basis
resulting in the ambient components , i.e.
The question is, how are
and
related?
In order to answer this question, substitute the identity
into the equation
which yields
This identity tells us that the
combination
represents the ambient coordinates of . In other words,
In this identity, the shift tensor plays a role that can be more accurately described as
"upshifting": translating the surface components of a tangent vector into its ambient components.
It is left as an exercise, which should be attempted after Section 3.8, to show that for a tangent vector with ambient components , the
surface components
can be recovered by contraction with the shift tensor on the ambient index, i.e.
3.7The length of a curve embedded in a surface
A curve embedded in a surface can be specified by the dependence of the surface coordinates
of the points on the curve on a parameter , i.e.
Our present goal is to express the
length of the curve by an integral in terms of the functions .
Recall from Chapter TBD of the Introduction to Tensor Calculus, that the length of a segment of a curve given by the vector equation
is expressed by the integral
Since the vector is tangential to the curve it is also
tangential to the surface in which the curve is embedded. Therefore, it can be expressed with
respect to both ambient and surface covariant bases. As we learned in Chapter TBD of Introduction
to Tensor Calculus, the contravariant components of are
where
are the ambient equations of the
curve. This conclusion follows from differentiating the identity
with respect to , i.e.
With the help of the components of
, the geometric integral
can be converted into the arithmetic
integral
as we established in Chapter TBD of
Introduction to Tensor Calculus.
Similarly, the surface components of are
as can be shown by differentiating
the identity
with respect to . We have
Therefore, the length of the curve
is also given by the formula
Thus, as we might have expected, the
length of a curve on a surface can be calculated by referring to its equation within the surface
and the surface covariant metric tensor, while ignoring how either object is embedded in the larger
ambient space.
3.8The relationship between the ambient and the surface metric tensors
The connection between the surface and the ambient basis, i.e.
immediately leads to the connection
between the surface and the ambient metric tensors. Indeed, since
we have
In summary,
The right side of this identity may
be described as having each of the subscripts of
operated on by the shift tensor.
The pivotal identity
can be written in a number of other
useful forms. Since
the first alternative form reads
If you prefer to see the index in important identities, you may rewrite the same
identity as
Finally, by raising the index , we arrive at
which is perhaps the most elegant
form of the same identity. This identity is usually written with the two sides reversed, i.e.
Interestingly, the identity that
relates the surface and the ambient metric tensors
and
features neither object explicitly.
We ought to remark on the identity
from the Linear Algebra point of
view. Both
and
correspond to matrices. If
corresponds to a matrix and
corresponds to the matrix , then the contraction
corresponds to the product . Since
corresponds to the identity matrix , the matrix equation has the following "shape":
Since each of the matrices is rank
, it is quite feasible that the product results in the
identity matrix.
On the other hand, if the same two matrices were multiplied in the opposite order, i.e. ,
the shape of the resulting identity would be
The rank of the product still cannot
be greater than and therefore the resulting matrix cannot be the identity matrix. Since
corresponds to the contraction ,
we conclude that the latter cannot equal ,
i.e.
However, we will soon discover that
satisfies the analogous identity
which involves the components of
the unit normal studied below.
3.9The relationship between the ambient and surface Christoffel symbols
Having related the ambient and the surface metric tensors, let us now relate the surface
Christoffel symbol
to its ambient counterpart .
Our analysis will yield an attractive identity that offers a practical way of calculating the
surface Christoffel symbol
in many situations.
Recall that the surface Christoffel symbol is given by
while the ambient Christoffel symbol
is given by
The key to connecting these
identities is of course the relationship
which expresses the surface basis
in
terms of the ambient basis .
Substituting
and in
the equation
we find
By the product rule,
It is left as an exercise to show
that
and therefore
Meanwhile,
Combining the above equations, we
find
The first term in this attractive
identity can be described as the shift of the ambient Christoffel symbol onto the surface.
Finally, note that when the ambient space is referred to affine coordinates where , the above identity simplifies to the equation
which is often used for practical
calculations of the surface Christoffel symbol.
3.10The components of the unit normal
Denote the components of the unit normal by , i.e.
or
Later in this Chapter, we will
demonstrate that, up to sign, the components are
given by the explicit formula
For the time being, however, we
would like see how much we can learn about
without this formula.
Recall that at each point on the surface, there are two unit normals that point in the opposite
directions. Correspondingly, the components can
have two opposite sets of values depending on the choice of normal. In any given situation, the
choice of normal is made a priori, either arbitrarily or according to some geometric
rationale. Once the choice is made, the normal may be considered unique and therefore an invariant. The
components are
then uniquely determined as well and represent a tensor with respect to changes in the ambient
coordinates.
Let us now determine the identities for the components that
correspond to the unit-length and orthogonality conditions
and
Of course, the component form of the
unit-length condition reads
In order to convert the
orthogonality condition to component form, note that since , we
have
Since
we have
Thus, in component form, the
orthogonality condition reads
It is left as an exercise to argue
that, collectively, the equations
determine up to
sign.
3.11Orthogonal projection onto the tangent plane
Earlier in this Chapter, we considered a tangent vector with surface components
and showed that its ambient components are
given by the equation
This time, consider a vector with components , i.e.
, that
is not tangent to the surface. The combination
still makes sense from the tensor
notation point of view. As our experience shows, feasible tensor combinations are almost always
worthwhile. What, then, is the geometric interpretation of the vector with surface components
In this Section, we will demonstrate
that it is the orthogonal projection of onto the tangent plane.
In Chapter 2, we showed that the surface components
of the orthogonal projection of onto the tangent plane are given by the dot product
Substituting , we
find
Since
we find
Thus, the combination
indeed represents the components
of the orthogonal projection of onto the tangent plane. As a result, the shift tensor
may be thought of geometrically as the orthogonal projection operator onto the tangent plane, as it
relates the ambient components of a vector to the surface components of its orthogonal projection
.
Let us now relate the ambient components of to the ambient components of . At the end of the previous Section,
we mentioned that the ambient coordinates of a
tangent vector are obtained by contracting its
surface components
with the shift tensor, i.e.
Since, as we have just established,
,
we have
Alternatively, we could have arrived at this relationship by starting with the identity
derived in Chapter 2. Then, upon substituting the expansions
we find
Since
we have
Equating the components of the
vectors on either side, we once again arrive at the relationship
Thus, the combination
may be thought of as the operator of
orthogonal projection onto the tangent plane. It should be noted that compactness of is
quite remarkable. Recall from Linear Algebra that the problem of finding the orthogonal projection
onto a linear subspace is solved by the technique of least squares. If is the rectangular matrix, then the operator of
orthogonal projection onto the column space of is given by the combination
The combination
includes all of the same elements -- however, the complexity of the operations is absorbed by the
indicial notation. In particular, the matrix
corresponds to the contravariant metric tensor
which makes its presence felt via the placement of the surface index in the shift tensor as
a superscript.
3.12Orthogonal projection away from the tangent plane
In Chapter 2, we showed that the orthogonal
projection of a vector onto the normal direction , i.e. away from the tangent plane, is given by
Let us convert this identity to
component form.
The dot product is given by .
If are
the ambient components of , then the above equation reads
Equating the components, we find
which is the relationship that we
set out to find. Whereas the combination
represented the operator of
orthogonal projection onto the tangent plane, the combination
represents the operator of
orthogonal projection away from the tangent plane. A good question to consider, then, is
what does the sum
represent? This question will
be answered in the following Section.
3.13The projection formula
Recall the identity
from Chapter 2 which states that a vector at a point on a
surface is the sum of its orthogonal projection onto
the tangent plane and its orthogonal projection away from the tangent plane. In component form, the above
identity reads
Substituting the combination
for on
the left, we find
Since the above identity holds for
any ,
we arrive at the relationship
known as the projection
formula. It is usually written with the Kronecker delta on the right, i.e.
Other useful forms of the projection
formula read
and
Earlier in this Chapter, we remarked
that the combination
cannot equal .
The projection formula refines that insight and identifies precisely the relationship of to
.
3.14An explicit expression for
As our experience so far has shown, we can work quite effectively with the components of
the unit normal even though they have only been specified implicitly by the orthogonality
condition
and the normalization condition
Of course, these conditions actually
give us a practical way of calculating . It
is left as an exercise to show that if is the matrix that represents the shift tensor ,
then
corresponds to a unit vector from the one-dimensional null space of .
Thus, an explicit expression for is
not needed. However, it is an intriguing challenge to find such an expression and we will do so in
this Section.
The inspiration for the expression comes from the concept of the cross product. Note that
the elements and
of the
surface covariant basis represent two linearly independent vectors in the tangent plane. Therefore,
their cross product
is orthogonal to the plane and is
therefore collinear with . Thus, all that is left to do is to find a vector of unit
length that is a scalar multiple of .
The ambient components of and
are
found in the elements of the shift tensor .
Specifically, the components of are
and those of are
.
Thus, as was described in Chapter TBD of Introduction to Tensor Calculus, the covariant
components of
are
given by the equation
It is left as a straightforward
exercise to confirm that
satisfies the orthogonality condition
However, in order to be
geometrically meaningful, must
be a tensor. Meanwhile, the expression
uses literal subscripts and , which are disallowed by the rules of the tensor
notation and thus , as
defined, is not a tensor. Fortunately, this difficulty is easy to overcome.
It is left as an exercise that the expression
is skew-symmetric with respect to exchanging the values of the literal indices, i.e.
Therefore, the difference
is twice and
therefore also represents a vector that is collinear with . With the help of the permutation symbol ,
this difference can be written in the form
Next, replace the permutation symbol
with the Levi-Civita symbol
in order to arrive at the tensor expression
Now, the only remaining questions are those of length and sign. It is left as an exercise to show
that the length of the vector with components above is . Thus, scaling the expression above by we arrive at
Of course, depending on our a
priori choice of , the above formula may deliver the components of rather than . Finally, we must note that the variant on the right side of
the above formula is a tensor only under orientation-preserving transformations of both ambient and
surface coordinates.
3.15Exercises
Exercise 3.1Show that the equations of the surface for a sphere of radius in cylindrical ambient coordinates read
Exercise 3.2Show that the equations of the surface for a cylinder of radius in spherical ambient coordinates read
Exercise 3.3In the text, we showed that the shift tensor is a tensor with the help of the identity
However, it is important to be able to demonstrate its tensor property on the basis of its definition
Do so in three steps. First, consider changes only of ambient coordinates. First justify and then use the identity
to show that
Second, consider changes of only surface coordinates and use the identity
to show that
Finally, consider simultaneous changes of ambient and surface coordinates. Use the identity
to show that
Exercise 3.4Suppose that the elements of are organized into a matrix . Show that the matrix consisting of the elements of belongs to the null space of . This observation gives a practical way of calculating the components .
Exercise 3.5Show that the length of the vector with components
is . In other words, show that if
then
Exercise 3.6Let
Show that
Notice that in the language of matrices, the above identity reads which represents the Linear Algebra definition of a projection matrix.
Exercise 3.7Similarly, let
and show that
Thus, the matrix corresponding to also satisfies the Linear Algebra definition of a projection matrix.
Exercise 3.8Show that the derivatives of the ambient covariant basis with respect to the surface coordinates are given by the formula
Exercise 3.9Derive the identity
from the intrinsic definitions of the Christoffel symbols
and
Exercise 3.10Notice the striking similarity between the definition of the surface Christoffel symbol
and the formula
valid for affine ambient coordinates. Derive the latter equation from the former by assuming affine coordinates in the ambient space from the start.
Exercise 3.11Use the explicit expression for to prove the projection formula
This is an important, albeit time-consuming, exercise that you should take your time working out.
Exercise 3.12Show that the length of one cycle of the cycloid is .