This entire Chapter is devoted to the exploration of the curvature tensor .
We will begin by recalling the key relationships involving the curvature tensor
that we have established in the earlier Chapters.
6.1Elementary identities and definitions
Our analytical exploration of curvature started with the realization that the spatial variability
of the surface covariant basis comes
from two sources: the potential non-uniformity of the surface coordinates
and the non-flatness -- in other words, curvature -- of the surface. While the
non-uniformity of the surface coordinates can be effectively managed by switching from partial to
covariant differentiation, the curvature of the surface is a matter of actual geometry. We
therefore embrace it rather than seek to eliminate it from consideration by some analytical device.
The opportunity to quantify curvature presented itself when we discovered that each of the vectors
in the tensor is
orthogonal to the surface and therefore collinear with the unit normal . We then assembled corresponding coefficients of
proportionality into a second-order system called the curvature tensor ,
i.e.
Dotting both sides of the above
equation with yields an explicit expression for
captured by the equation
Since the covariant basis is
the derivative of the position vector , i.e.
the above identities may also be
written in forms
and
in terms of the second derivatives
of . Note that while, in general, the covariant derivatives and
do
not commute, they do commute when applied to a variant of order zero. Indeed, for a
zeroth-order variant , we have
Since the Christoffel symbol is
symmetric in its subscripts, i.e.
both of the terms in the expression
for are symmetric in and and therefore
Therefore is symmetric, i.e.
In other words,
from which it follows that the
curvature tensor is
symmetric, i.e.
or, equivalently,
Because of the symmetry of the
curvature tensor, its mixed form
can be written in this simplified form without the use of the dot placeholder. This subtle point
was discussed in Chapter TBD of Introduction to Tensor Calculus. Finally, recall that, as we
discussed in Chapter 2, the covariant derivative in
the identity
may be replaced with the partial derivative, i.e.
In Chapter 5, we observed that
can be computed in the component space by the equation
and the Weingarten equation
where
is the shift tensor obtained by differentiating the equations of the surface , i.e.
Importantly, the "sign" of the curvature tensor depends on the choice of normal. Recall that there
are two unit normals pointing in opposite directions and, as we agreed in Chapter 2, the symbol represents either one of them. Thus, depending on the choice
of normal, the resulting elements in the tensor
may summarily change sign. As a result, the curvature tensor inherits the same sign ambiguity of
the unit normal. By extension, the same is true of the mean curvature . The
Gaussian curvature , on the other hand, being the
determinant of the matrix corresponding to ,
is unchanged when the sign of the matrix is flipped and is therefore independent of the choice of
normal. The product ,
known as the vector curvature tensor, is also independent of the choice of normal since both
elements in the product change sign when the normal is reversed.
6.2The invariants of the curvature tensor
This Section calls for a brief Linear Algebra preamble. As we described in Chapter TBD of
Introduction to Tensor Calculus, a matrix representing a linear transformation corresponds to a
mixed second-order tensor .
Such a matrix is characterized by fundamental invariants -- its eigenvalues , , , . From
these invariants, numerous others can be constructed. Two of the most noteworthy such invariants
are the sum of the eigenvalues, which equals the trace of , i.e.
and their product, which
equals the determinant, i.e.
While the eigenvalues of a general
matrix may be difficult to calculate (in fact, no finite
algorithm for calculating eigenvalues is possible for a matrix of dimension greater than ), the trace and the determinant are readily available.
For a self-adjoint transformation characterized by a symmetric tensor ,
i.e.
all eigenvalues are real and the
corresponding eigenvectors are orthogonal -- or, in the case of repeated eigenvalues, can be
chosen to be orthogonal. The eigenvectors represent the critical points of the quadratic
form
subject to the unit-length
constraint
When we transfer these facts onto the curvature tensor ,
we find that each of the objects mentioned above are of great geometric importance. The eigenvalues
and
are
known as the principal curvatures while the corresponding eigenvectors are known as the
principal directions. The sum is, of
course, the mean curvature while
their product is, of
course, the Gaussian curvature. We will now take a detailed look into each of these
elements, starting with mean curvature.
6.2.1The mean curvature
The invariant
is known as the mean
curvature of the surface. The mean curvature is often denoted by the letter but we will almost always prefer the symbol .
The mean curvature is a particularly important invariant that appears in many fundamental
identities. It is, by virtue of its ubiquity, the star of our entire narrative. Many physical
phenomena associated with capillary pressure (i.e. the pressure differential across an interface
between two fluids) are described by equations that invariably feature the mean curvature. Thus,
not surprisingly, it plays an important role in the dynamics of fluid films. Furthermore, mean
curvature plays an important role in the study of minimal surfaces, i.e. surfaces with a
given boundary that have the least possible area. As we will demonstrate in a future book on the
Calculus of Moving Surfaces, minimal surfaces are characterized by zero mean curvature.
The vector can
be referred to as the vector mean curvature or, by analogy with curves that we will discover
in Chapter 8, as the curvature normal. As we
learned in Chapter 2, it equals the surface
divergence of the covariant basis
or the surface Laplacian of the position vector , i.e.
Thus, an alternative expression for
the mean curvature is
The advantage of these identities
is, of course, their pure geometric nature. For example, the first of the two equations will
readily explain why the integral of the curvature normal over a closed surface is zero.
6.2.2The Gaussian curvature
The determinant of the mixed curvature tensor
of a two-dimensional surface is the Gaussian curvature . However, this is not the
definition of Gaussian curvature but rather a consequence of the Gauss equations which we
mentioned in Chapter 2 and will describe in detail
in Chapter 7. As we stated in Chapter 2, by definition, the Gaussian curvature is the
invariant in the two-dimensional identity
where is
the Riemann-Christoffel tensor. Meanwhile, as we showed in Chapter TBD of Introduction to Tensor
Calculus, any second-order system
in a two-dimensional space satisfies the equation
Now, this is where the Gauss
equations enter. From the Gauss equations
we conclude that
and therefore
We will save the rest of our discussion of Gaussian curvature for Chapter 7.
6.2.3The principal curvatures
The eigenvalues of
are known as the principal curvatures. Thus, two-dimensional surfaces are characterized by
two eigenvalues, and
. As
mentioned earlier, the principal curvatures and
correspond to the minimum and the maximum values of the quadratic form
subject to the unit normalization
condition
Furthermore their sum is the mean
curvature, i.e.
and their product is the determinant
of
which, by the Gauss equations, equals the Gaussian curvature , i.e.
The geometric interpretation of the
principal curvatures and
and
the corresponding eigenvectors will be described below in a Section devoted entirely to that topic.
Note that some texts define the mean curvature as the average of the principal curvatures,
i.e.
which explains the use of the word
mean in mean curvature. Such a definition has some advantages over our definition.
For example, as we demonstrate below, the mean curvature of a
sphere of radius is which, in dimensions, generalizes to . The definition based on the average,
on the other hand, yields the value of in all dimensions. Nevertheless, we
will stick with our definition since, in numerous applications, including the Calculus of Moving
Surfaces, it is ,
rather than , that is most frequently encountered.
6.2.4The third fundamental tensor of a surface
The metric tensor is
sometimes referred to as the first fundamental tensor of the surface while the curvature
tensor is
referred to as the second fundamental tensor. The third fundamental tensor ,
which arises frequently in applications, is the tensor
defined by the equation
In other words,
corresponds to the matrix square of the curvature tensor. Note that the fundamental tensors often
figure as binlinear forms, such as .
For this reason, they can also be referred to as fundamental forms or groundforms.
It is left as an exercise to show that
Note the similarity among the equations that can act as definitions of the first groundform ,
the second groundform ,
and the third groundform ,
especially if we denote by and
by . Then
we have
As we know from Linear Algebra, the eigenvalues of
are .
Therefore, the invariant is
given by
while the determinant of
is given by
6.2.5The special case of planar curves
We have already studied planar curves in Chapter TBD of Introduction to Tensor Caclulus,
where our analysis was based on parameterizing the curve by the arc length . We will now approach curves from a different angle --
that is, as a special one-dimensional case of an embedded surface. In other words, we will, to the
extent possible, ignore their one-dimensional nature and focus on what the general theory of
surfaces can tell us about them.
A planar curve is a curve embedded in a Euclidean space. Therefore, the dimension of a planar curve
trails that of its ambient space by , which makes it a hypersurface. As a hypersurface, it is
characterized by a unique (within sign) unit normal . Thus, the concept of the curvature tensor applies in full
force, as is the concept of mean curvature. The curvature tensor is
still defined by the equation
or, equivalently,
while the mean curvature is
given by
or, equivalently,
Compare this equation to the
identity
from Chapter TBD of Introduction
to Tensor Caclulus, where is signed curvature and is the unit tangent as a
function of the arc length . Since, as it is left as an exercise to show,
is equivalent to , we observe that for planar
curves, the concept of mean curvature is equivalent to that of signed curvature.
Below, we will calculate the curvature tensor as well as the mean curvature for general planar
curves represented in Cartesian and polar coordinates.
6.3The geometric interpretation of the principal curvatures
The geometric interpretation of principal curvatures involves curves embedded in two-dimensional
surfaces. This configuration creates a fascinating interplay among three spaces: the
one-dimensional curve, the two-dimensional surface, and the three-dimensional ambient Euclidean
space. This intricate arrangement will yield a great number of intriguing relationships and
insights. Some of these will appear in this book, but a great many more are beyond our scope -- and
many more still are yet to be discovered.
Note that we have not yet developed a theory of surfaces embedded in non-Euclidean spaces, which is
what a curve embedded in a general two-dimensional surface represents. Such a theory will be
developed in Chapter 9. Fortunately, in order to
understand the geometric interpretation of principal curvatures, we will only need to consider
planar curves which, as we saw in the previous Section, we already have under our belt.
A planar curve arises when a surface is cut by a plane, as illustrated in the following figure.
 (6.32) Our analysis will focus on a single point which lies on the curve at the
intersection of the surface and the cutting plane. Furthermore, we will assume that the cutting
plane is orthogonal to the surface at the point . In other words, the cutting plane
contains within in it the surface normal at .
(6.32) Our analysis will focus on a single point which lies on the curve at the
intersection of the surface and the cutting plane. Furthermore, we will assume that the cutting
plane is orthogonal to the surface at the point . In other words, the cutting plane
contains within in it the surface normal at . 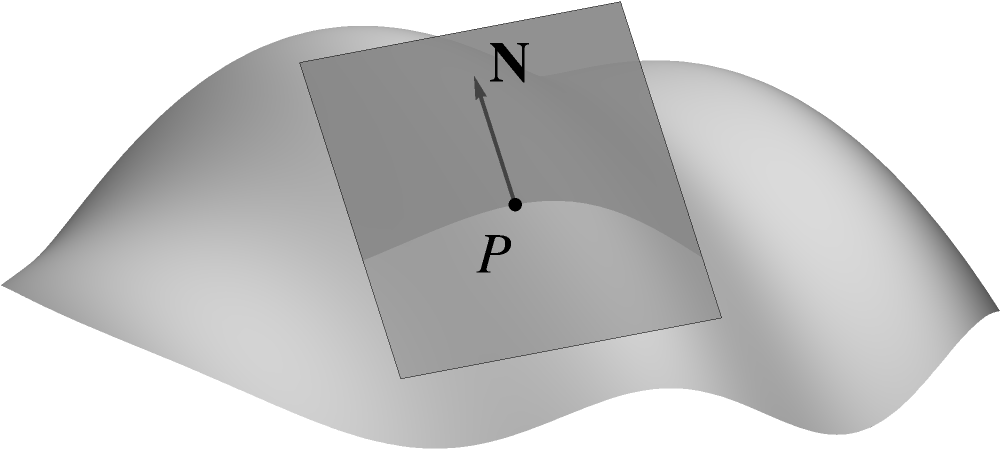 (6.33) This condition does not specify the plane uniquely as there is
an entire family of such planes obtained by rotation about the straight line containing .
(6.33) This condition does not specify the plane uniquely as there is
an entire family of such planes obtained by rotation about the straight line containing .
 (6.32)
(6.32) (6.33)
(6.33)The curve at the intersection of the surface and the plane can be analyzed from three distinct
points of view. First, it can be viewed as a curve embedded in the two-dimensional surface. In this
context, the surface can be described as the ambient space with respect to the curve.
Second, it can be viewed as a curve embedded in the overall three-dimensional Euclidean space. And
finally, it can be viewed as a curve embedded in the two-dimensional Euclidean cutting plane.
Naturally, it is the last embedding with which we will concern ourselves here.
The curve represents a hypersurface with the respect to the plane. It is therefore characterized by
its signed curvature which, as we observed in the previous section, is
equivalent to its mean curvature in the context of its embedding in the plane. Naturally, depends on two characteristics: the curvature
characteristics of the ambient surface and the orientation of the cutting plane. In this Section,
we will succeed in capturing these dependencies by the elegant equation
where
are the surface components of the unit tangent to the curve. Clearly, the curvature tensor
captures the curvature characteristics of the surface while the tangent captures the orientation of the surface. The reader is
invited to attempt deriving this identity on their own before we lay out the details below, as it
relies on the techniques that we have developed earlier.
Before we turn to the derivation of the above identity, let us make one important geometric
observation that will prove relevant later. Consider the unit normal to the curve when
viewed as a hypersurface within the cutting plane. At the point , and likely only at the point
, it is colinear with the surface
normal . This is by construction: the surface normal at the point is orthogonal to all curves in
the surface that pass through , including the one formed by the
intersection of the surface and the plane. The same cannot be said for any other point on the curve
since there is no guarantee that the surface normal is contained within the cutting plane.
Despite our present affinity for treating curves as a special case of surfaces, we will, for the
remainder of this Section, return to the style of analysis based on parameterizing the curve by its
arc length , which we employed in Chapter TBD of Introduction to
Tensor Calculus. As before, denote the function representing the position vector at the points on the curve by , i.e.
Recall that the first derivative of
is the unit tangent , i.e.
while the second derivative is the curvature normal , i.e.
(Note that the determinant of the surface curvature tensor
is unrelated to the magnitude of the vector .) Importantly, for all , the vectors and both lie within the cutting
plane. Meanwhile, the curvature normal is collinear with the in-plane normal to the curve which
coincides with the surface normal at the point . Thus, at the point , the signed curvature , given by the identity
is also given by the identity
All but the last equation in the previous paragraph are characteristic of the curve with respect to
its embedding in the cutting plane. Thus, in order to derive the equation
we must find a meaningful way to
engage the differential characteristic of the surface.
Suppose that the curve within the surface is given by the equations
Then the function can be constructed by composing
the function , i.e. as a function of the surface coordinates ,
with the equations of the curve , i.e.
As we always do after establishing a
relationship such as above, we will differentiate both sides with respect to the independent
variable, i.e. the arc length . By the chain rule, we have
On the left, we recognize as the unit tangent . On the right, the partial derivative
is, of course, the surface covariant basis . In
other words, we have obtained the identity
which tells us that the derivatives
of the equations of the curve can be interpreted
as the surface coordinates
of . In this respect, the equation
is similar to a number of identities we have derived in the past, such as
in Chapter TBD of Introduction to Tensor Calculus.
In order to get to curvature, we must differentiate the identity
a second time. By the product rule,
As we recalled above, the derivative
is the curvature normal . Meanwhile, on the right, the object of utmost interest is
the derivative
which captures the rate of change of
the covariant surface basis along
the curve. Similarly to , the function can be constructed by
substituting the equations of the curve into , i.e.
Then, by the chain rule, we have
The derivative
is where the curvature tensor makes its appearance. Since
and by definition of the covariant
derivative
we find
Thus,
becomes
and therefore
becomes
where we have dropped the arguments
of the functions for the sake of conciseness. Combining normal and tangential terms, we find
On the one hand, the combination
which represents the tangential
component of the curvature normal , is quite intriguing as it reminds us of the
-derivative introduced in Section TBD of Introduction
to Tensor Calculus. It will also reemerge in the future as we study the concept of the geodesic
curvature for curves embedded in surfaces. On the other hand, since the curvature normal is colinear with the surface normal at the point as we established above, we can
conclude that the tangential component of vanishes, i.e.
Therefore, the curvature normal
is given by
Finally, since
we arrive at the identity
In other words,
as we set out to show.
The geometric interpretation of the principal curvatures and
follows immediately from the identity 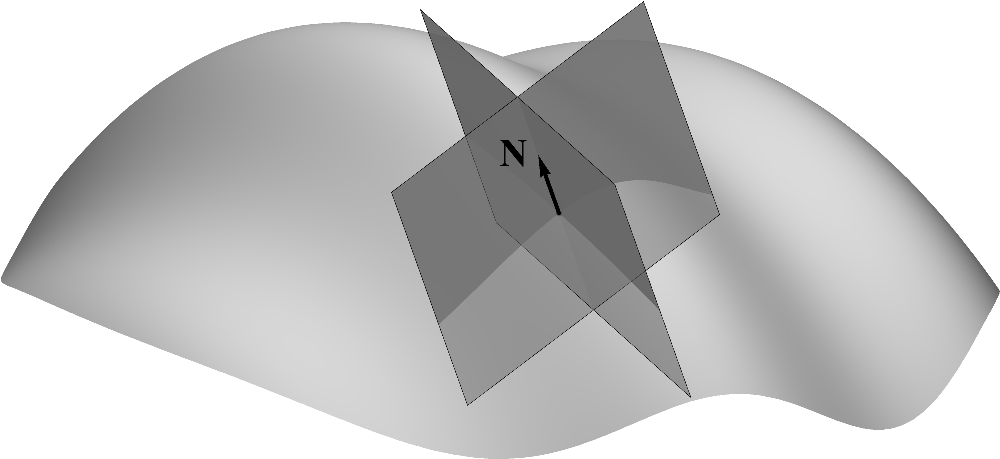 (6.62) The following figure shows a point
where the interplay between the principal curvatures is more interesting -- one is positive and the
other is negative.
(6.62) The following figure shows a point
where the interplay between the principal curvatures is more interesting -- one is positive and the
other is negative.  (6.63)
(6.63)
Recall that the principal curvatures
and
of a
surface are defined as the eigenvalues of .
From Linear Algebra, we know that these values are precisely the least and greatest values of the
quadratic form
subject to the constraint
Therefore, the principal curvatures
correspond to the least and the greatest signed curvatures of curves formed by intersecting the
surface with orthogonal planes. Such values always exist and the corresponding directions,
characterized by the unit tangents and
are
orthogonal. The following figure shows the two cutting planes corresponding to the principal
directions.
 (6.62)
(6.62) (6.63)
(6.63)This interpretation of the principal curvatures immediately tells us the curvature invariants on
the sphere of radius . 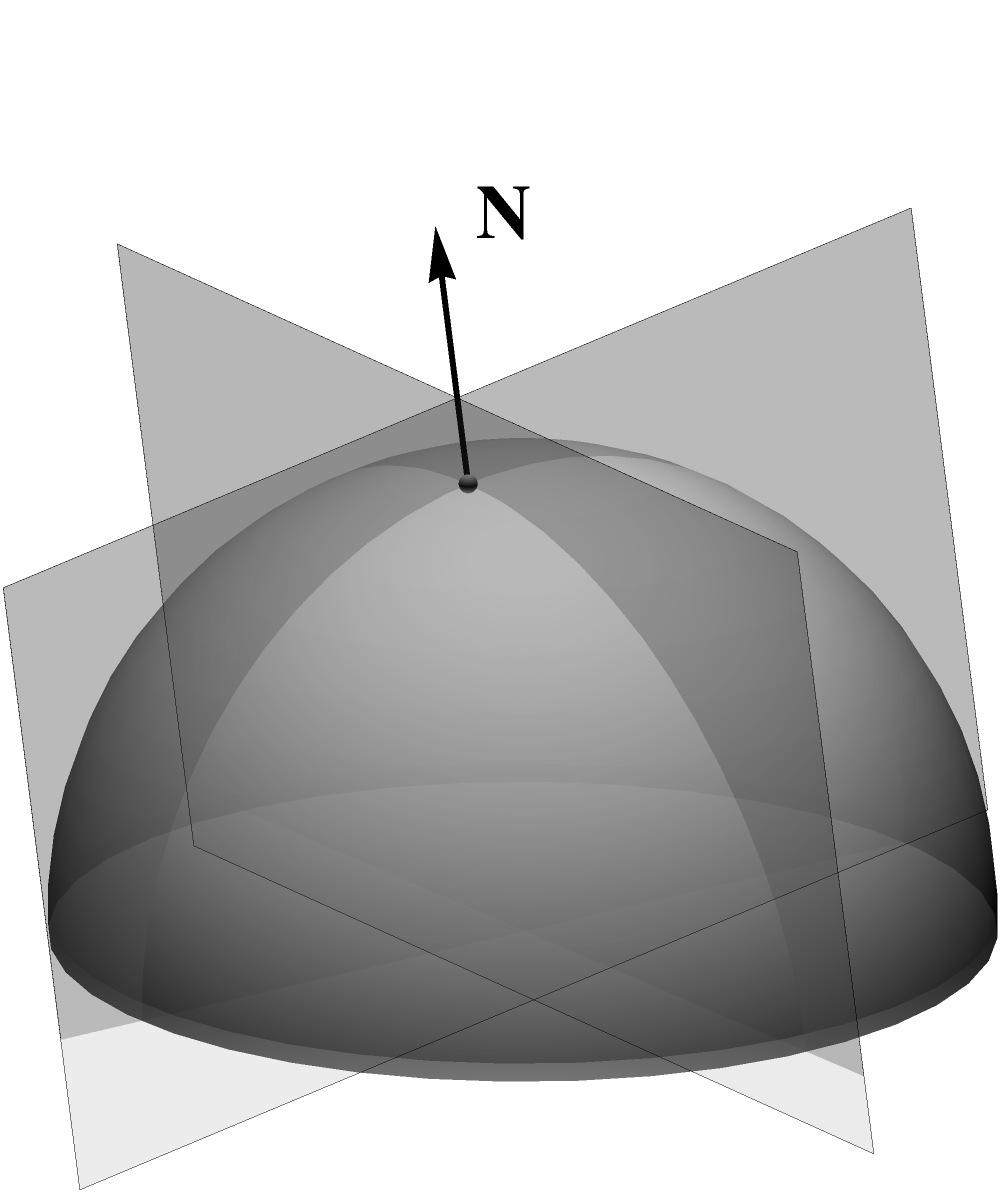 (6.64) A normal plane cuts the sphere in a great circle of radius
. Thus, with respect to the outward
normal, for both principal curvatures, we have
(6.64) A normal plane cuts the sphere in a great circle of radius
. Thus, with respect to the outward
normal, for both principal curvatures, we have
 (6.64)
(6.64) Thus, the mean curvature of the
sphere with radius with respect to the outward normal is
given by
The Gaussian curvature , which is independent of the choice
of normal, is given by
6.4Calculation of the curvature tensor for several two-dimensional surfaces
In this Section, we will expand the analyses presented in Chapter 4 to include the curvature tensor. One of the more convenient ways to
calculate the curvature tensor by hand is represented by the form
of Weingarten's equation. When the
ambient space is referred to Cartesian coordinates,
coincides with the partial derivative
and the expression for the curvature tensor
becomes
This identity corresponds to a
product of two matrices which, leveraging the notation introduced in Chapter 4, reads
6.4.1A sphere of radius
For a sphere of radius referred to coordinates and embedded in a Euclidean space referred to Cartesian
coordinates, recall the following values:
Note that the components in
the above table correspond to the outward normal.
Differentiating the components of the normal with respect to the surface coordinates, we find
Therefore, for the curvature tensor
,
we have
Raising the index and, subsequently, , we find
From the expression for ,
we can confirm our earlier calculation of the mean curvature , i.e.
Finally, the principal curvatures
and
are
given by
Note that the values of the
curvature tensors, the mean curvature, and the principal curvatures correspond to the outward
normal and would have the opposite sign had the other normal been selected.
6.4.2A cylinder of radius
Recall that
Thus,
and therefore the various forms of
the curvature tensors are as follows:
From ,
we see that the mean curvature is
given by
Finally, the principal curvatures
are given by
6.4.3A torus with radii and
Recall that
Thus,
As a result, the various forms of
the curvature tensor are
From ,
we see that the mean curvature is
given by
Finally, the principal curvatures
are given by
6.4.4A surface of revolution
Consider a surface of revolution given by the functions and as described in Sections 3.2.3 and 4.3, and
let ,
,
,
and
denote the derivatives of the functions and . Recall that
We have
As a result, the various forms of
the curvature tensor are
Therefore, the mean curvature is
given by
For the special case
used very commonly in applications,
we have
Meanwhile, the mean curvature is given by
and the principal curvatures are
6.5Calculation of the curvature tensor for planar curves
6.5.1In Cartesian coordinates
Recall, that for a general planar curve described in Cartesian coordinates by the equations
we have
Thus,
As a result, the various forms of
the curvature tensor are
The mean curvature
equals the sole element of ,
i.e.
Let us now document two special cases. When arc length is used to parameterize the curve, we have
and is,
of course, given by
If the curve is given by the graph
of a function , then we have
The mean curvature
equals the sole element of ,
i.e.
6.5.2In polar coordinates
For a general planar curve described in polar coordinates by the equations
the expressions for the mean curvature are too cumbersome to give here. We will therefore restrict
ourselves to curves that represent graph of function . It is left as an exercise to show that the
various forms of the curvature tensor are given by
In particular, the mean curvature
equals the sole element of ,
i.e.
6.6The mean curvature of an implicit surface
In this Section, we will demonstrate how to calculate the mean curvature of a
surface specified by an implicit equation
where is a function of the ambient coordinates
and
is a constant. In other words, the surface is a level
set of the function . The goal is to express in
terms of the covariant derivatives of
The following figure illustrates an implicit surface in an ambient space referred to Cartesian
coordinates.
(6.122)
To be clear, our
analysis will apply to arbitrary ambient coordinates. The above figure features Cartesian
coordinates only for the sake of visual clarity.
Naturally, we are not able to calculate to full curvature tensor
since the posed problem does not allow for surface coordinates .
On the other hand, the task of finding an expression for the mean curvature in
terms of the derivatives of should be feasible since is an
invariant characteristic of the surface. In other words, it is independent of the choice of
the surface coordinates .
Nevertheless, in order to find such an expression for , we
may still introduce a surface coordinate system ,
as long as we make sure that the final expression is free of any traces of it.
With the help of temporary surface coordinates ,
represent the surface by the equations
Plugging in these equation of the
surface into the implicit equation
we obtain the identity
in the surface coordinates .
Differentiating with ,
we find
or, equivalently,
Comparing this identity with the
definition of the unit normal
we recognize that must is a scalar multiple
of .
Therefore,
Note that by adopting this equation
over the alternative
we have selected one of the two
available normal directions.
In order to go from the unit normal to the curvature tensor, recall the corollary
of Weingarten's equation. By a
formal application of the chain rule to , we
have
and therefore
Here we must pause and note that,
ordinarily, the combination is
nonsensical since is
defined only on the surface and not in the surrounding ambient space, and is therefore not subject
to the ambient covariant derivative. In the present context, however, we can extend the normal
field to
the surrounding space by interpreting the implicit equation
not as a single surface
corresponding to a single value of , but as a family of surfaces corresponding to a
range of values of . Then the corresponding family of surface normals fills
the surrounding ambient space, as illustrated in the following figure, and we may therefore treat
as a
spatial tensor field subject to the ambient covariant derivative.
(6.132)
In the context of this interpretation of the object , the
formula
is justified. Contracting on and , we find
By the projection formula
we have
or, equivalently,
Note that with this equation, we
have already accomplished the goal of expressing in
terms of the covariant derivatives of since we already have such an
expression for .
However, we can greatly simplify this equation by showing that the second term term on the right
vanishes.
This is so because the combination
represents the derivative of a unit vector analogous to the blueprint example discussed in Section
TBD of Introduction to Tensor Calculus. Recall that the unit-length condition for the normal
reads
An application of the covariant
derivative to
both sides yields
Since the two terms of the left are
equivalent, we find
as we set out to show.
Thus, in terms of , the
mean curvature is
given by the remarkably simple expression
Recalling that
gives us the explicit expression for
in
terms of the covariant derivatives of , i.e.
We have therefore accomplished our
objective.
It is left as an exercise to show that the above equation is equivalent to
If we denote by and
by ,
then the above equation reads
It is also left as an exercise to show that, in terms of , the
trace of
the third groundform is
given by
Therefore, the Gaussian curvature
of a is given by
6.7Exercises
Exercise 6.1Show that
Exercise 6.3Show that at points where the mean curvature is zero,
Exercise 6.4Show that the catenoid, which is a shape of revolution given by the equation
has zero mean curvature.
Exercise 6.5Show that for a sphere,
in any surface coordinate system.
Exercise 6.6Show that various forms of the curvature tensor for a cone of angle are given by equations
Thus, the mean curvature is given by
while the Gaussian curvature vanishes, i.e.
6.7.1The tangent developable of a curve
The tangent developable of a curve is the surface swept out by tangent lines to the curve.
If the curve is given by the vector equation
then the vector equation for the
tangent developable reads
For the sake of simplicity, assume
that the curve is parameterized by the arc length . Recall that the derivative is the unit tangent , i.e.
and that the derivatives of are governed by the Frenet
equations
where is the principal normal, is the binormal, is the absolute curvature, is the torsion and the subscript denotes differentiation with respect to the arc length
.
Exercise 6.7Show that the covariant basis is given by
Exercise 6.8Show that the surface normal is collinear with the binormal an may therefore be chosen so that it coincides with , i.e.
Exercise 6.9Show that the covariant metric tensor is given by
and therefore the contravariant basis is given by
Meanwhile, the area element is given by
Exercise 6.10Show that the curvature tensors and , that correspond to the choice of the normal that coincides with , are given by
Thus, the mean curvature is given by
Recall that the surface Christoffel symbols are not needed for this calculation since is given by the idntity
which includes only partial derivatives.
6.7.2The polar developable
The polar developable of a curve is the surface swept out by axes of the osculating circles.
Thus, if the curve is given by the vector equation
then the vector equation for the
tangent developable reads
Let
begin{exercise} Show that the covariant basis vectors are given by
end{exercise}
Exercise 6.11Show that the surface normal corresponds to the tangent , i.e.
Exercise 6.12Show that the covariant metric tensor is given by
and the contravariant metric tensor is given by
Exercise 6.13Show that the nonzero elements of the Christoffel symbol are
Exercise 6.14Show that the curvature tensors and , that correspond to the choice of the normal that coincides with , are given by
Thus, the mean curvature is given by
6.7.3The -derivative
The next set of exercises analyzes the motion of a particle along a trajectory embedded in a
surface. The trajectory is described by the equations
that specify the surface coordinates
as a function of time .
Exercise 6.15Show that the surface components of the particle's velocity are given by ordinary time derivatives of , i.e.
Hint: .
Exercise 6.16 Show that the acceleration of the particle is given by
where
Conclude that is a tensor with respect to coordinate transformations on the surface.
Exercise 6.17Note that the term
corresponds to centripetal acceleration. It is a generalization of the familiar expression
for the centripetal acceleration of a particle moving with uniform speed around a circle of radius . In fact, show that for a sphere of radius , we have
where is the magnitude of the velocity vector , i.e.
Exercise 6.18Inspired by equation
define the -derivative along the trajectory according to the equation
In his Application of Tensor Calculus, A.J. McConnell refers to this operator as the intrinsic derivative, but we will prefer the term -derivative. Show that the -derivative satisfies the tensor property.
Exercise 6.19Show that the -derivative satisfies the product rule.
Exercise 6.20Show that the -derivative commutes with contraction.
Exercise 6.21Show that for a time-dependent variant defined on the broader surface, the -derivative satisfies the chain rule
Exercise 6.22Conclude that the -derivative is metrinilic with respect to all the surface metrics, except and . Meanwhile,
Exercise 6.23Use the newly developed calculus to rederive the equation
Exercise 6.24Show that the jolt is given by the formula
6.7.4Implicit surfaces
The next set of problems concerns surfaces specified by the implicit equation
Define the tensor
according to the equation
The object
may be referred to as the upshifted curvature tensor.
Exercise 6.25Show that is symmetric, i.e.
Exercise 6.26Show that
Exercise 6.27Show that
Exercise 6.28Show that
or
Exercise 6.29With the help of the equation
show that the Gaussian curvature is given by
or
Exercise 6.30Test the formulas derived in Section 6.6 for a sphere of radius , implicitly specified in Cartesian coordinates by the equation
Exercise 6.31In Cartesian coordinates, an egg-shaped ellipsoid with semi-axes , , and is given by the implicit equation
Derive the expressions in terms of , , and for its mean curvature and Gaussian curvature .