In Introduction to Tensor Calculus, our initial approach to Euclidean spaces was largely
geometric as we proceeded as far as possible without introducing coordinates. Recall, however, that
when it came to the analysis of curves embedded in a Euclidean space, we did introduce a parameter
along the curve. This allowed us to
define all the relevant differential objects but did not give us the ability to
calculate them for virtually any curve. That ability comes, of course, with the introduction
of coordinates in the surrounding space. Overall, our approach proved an optimal compromise between
pure geometric and all-out coordinate approaches as it enabled us to continue using our geometric
intuition while providing us with a reasonably robust analytical framework.
Our approach to surfaces will mimic our approach to curves. That is, we will introduce a coordinate
system on the surface itself but will leave the surrounding Euclidean space coordinate-free. The
Euclidean nature of our approach will initially limit us to three dimensions. This leaves us with
three configurations: surfaces in a three-dimensional space, curves in a two-dimensional space, and
curves in a three-dimensional case. We will start with two-dimensional surfaces and we will later
find it to be easy to carry over various parts of our analysis to other configurations, including
surfaces in a higher-dimensional arithmetic Euclidean space, as described in Chapter TBD of
Introduction to Tensor Calculus.
In this Chapter, we will cover the same topics as several chapters of Introduction to
Tensor Calculus. We will introduce all of the surface analogues of the metrics, the surface
Christoffel symbol, the Levi-Civita symbols, covariant differentiation, as well as the surface
analogues of invariant differential operators such as the Laplacian and the divergence. It will be
possible to cover so much ground because we will closely follow our own Euclidean blueprint.
Derivations of virtually all of the analogous facts will either be delegated to exercises or
skipped altogether. Of course, the reader is invited to justify all of the statements that we will
make which, in most cases, can be accomplished by imitating what we did in the context of Euclidean
spaces.
Naturally, the most exciting moments will be those where surfaces deviate from Euclidean spaces.
Most of those will be associated with the concept that is central to nature of surfaces --
curvature! -- which will occupy much of our narrative on surfaces. In this Chapter, we will lay the
foundation for our future investigations of this pivotal concept. Our exploration of curvature will
yield some of the most remarkable results in our entire subject.
2.1Pure geometric aspects of surfaces
Let us agree to accept the concept of a surface without a definition. The surrounding Euclidean
space will be referred to as the ambient space. As a whole, a surface is characterized by
its shape. Locally, the shape of a surface is described by its curvature which, as we
have just stated, is the primary object of our study.  (2.1) Due
to curvature, most surfaces cannot accommodate straight lines. In other words, surfaces do not
possess the kind of straightness that underpinned the concept of a Euclidean space. In particular,
we cannot discuss geometric vectors on surfaces, since a vector with its tail on the surface will
likely not be contained within the surface.
(2.1) Due
to curvature, most surfaces cannot accommodate straight lines. In other words, surfaces do not
possess the kind of straightness that underpinned the concept of a Euclidean space. In particular,
we cannot discuss geometric vectors on surfaces, since a vector with its tail on the surface will
likely not be contained within the surface.
 (2.1)
(2.1)To every point on a smooth surface, there corresponds a unique tangent plane -- another
concept that we will agree to accept without a definition for now but will later give an analytical
characterization that will agree with our intuition.  (2.2) A vector pointing in the unique direction orthogonal to the
tangent plane is known as a normal vector.
(2.2) A vector pointing in the unique direction orthogonal to the
tangent plane is known as a normal vector. 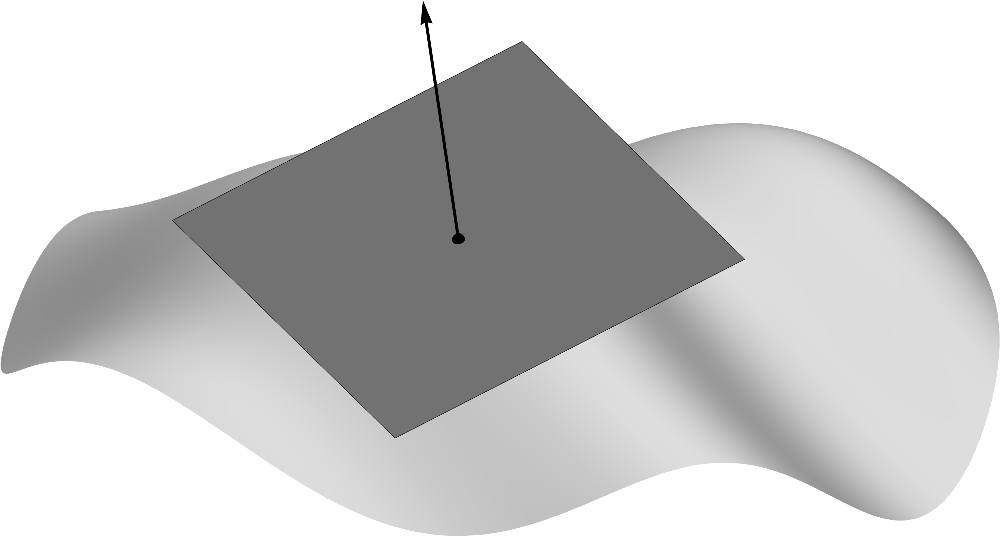 (2.3) A normal vector of length is known as a unit normal and is denoted by . With the help of the dot product, the fact that is unit length is captured by the equation
(2.3) A normal vector of length is known as a unit normal and is denoted by . With the help of the dot product, the fact that is unit length is captured by the equation
 (2.2)
(2.2) (2.3)
(2.3)We called a unit normal, with emphasis on a. The
indefinite article is appropriate since there are two opposite unit normals at every point. The
symbol can denote either one of the two unit normals. However, in
most analyses, a specific one of the two normals is selected, either arbitrarily or according to
some geometric, typically coordinate-free, criterion. In those situations, the phrase the unit
normal is typically used, even if the final selection has not yet
been made. 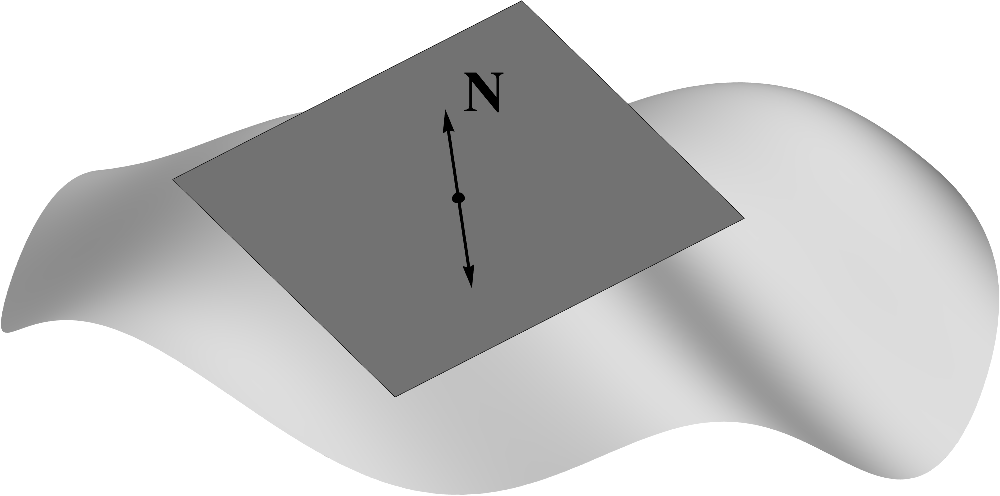 (2.5)
(2.5)
 (2.5)
(2.5) What makes normal direction unique is the fact that a two-dimensional surface embedded in a
three-dimensional space trails the dimension of the ambient space by . Embedded objects whose dimension trails that of the
ambient space by are known as hypersurfaces. Another example of a
hypersurface that we will describe in this Chapter is a planar curve, i.e. a curve embedded
in a plane.
This is about all that we are able to say about surfaces from a purely geometric point of view.
Further progress demands that we impose a coordinate system upon the surface.
2.2Surface coordinates
In order to enumerate the points of a two-dimensional surface, we need two coordinates. The surface
coordinates will be denoted by the symbols and
or,
collectively, .
We have switched to the Greek alphabet because the number of coordinates on the surface is
different from that in the ambient space for which we will continue to use Latin indices. In the
context of two-dimensional surfaces, all Greek indices will range from to .  (2.6)
(2.6)
 (2.6)
(2.6)For a canonical example, consider the surface of a sphere of radius . Introduce the coordinates and as illustrated in the following figure. 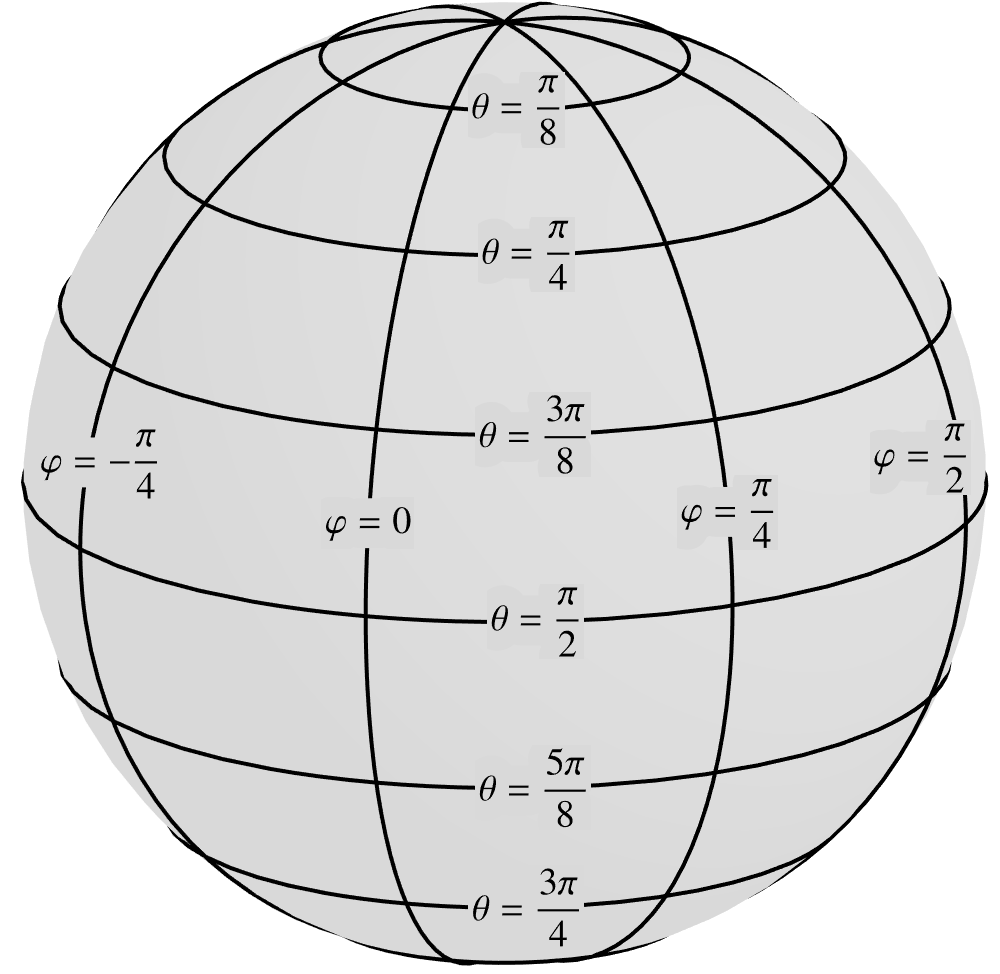 (2.7) To make sense of these coordinates,
simply imagine spherical coordinates in the ambient space and think of the sphere is the
coordinate surface corresponding to the fixed value of . Then the varying values of the
remaining coordinates and act as the surface coordinates and
.
(2.7) To make sense of these coordinates,
simply imagine spherical coordinates in the ambient space and think of the sphere is the
coordinate surface corresponding to the fixed value of . Then the varying values of the
remaining coordinates and act as the surface coordinates and
.
 (2.7)
(2.7)Importantly, the shape of the surface has significant influence on the way in which coordinates may
be assigned. In particular, we may not be able to achieve some desired regularity, as we did with
affine coordinates in the Euclidean space. Although we ought to clarify what we mean by
regular , it is nevertheless clear that the presence of curvature imposes some
constraints on the coordinate system. This insight alerts us to the fact that one of the central
conclusions that we reached for Euclidean spaces may not hold on surfaces. Namely, our ability to
choose an affine coordinate system in a Euclidean space leads to the Riemann-Christoffel equation
where is
the Riemann-Christoffel tensor given by
If we are able to build an
analytical framework that parallels the one we constructed for Euclidean spaces, we can expect the
analogue of the Riemann-Christoffel tensor will reveal to us something about curvature. I hope that
the thrill of anticipation of a new discovery is beginning to set in.
2.3Surface tensors
We will now do first what we previously did nearly at the end of our Euclidean space
narrative: define tensors. The concept of a tensor will apply to variants defined on the
surface. Consequently, the term surface tensor is often used to describe them, although we
will almost always prefer tensor for short. The definition of a tensor will not surprise you
since it will be exactly analogous to that of a Euclidean tensor. Suppose that the unprimed and
primed coordinates
and
are related by the identities
Introduce the Jacobians and
associated with this coordinate transformation
The two Jacobians are the matrix inverses of each other, i.e.
For future reference, the second
order Jacobians
and
are defined by
A variant ,
with a representative collection of indices, defined on the surface is an (absolute) tensor
with respect to coordinate changes on the surface if its primed and unprimed values are related by
the identity
More generally, it is a relative
tensor of weight if
where is the matrix representing . It
is left as an exercise to show that surface tensors satisfy all of the familiar properties of
Euclidean tensors. Namely, the tensor property is reflexive, symmetric, and transitive.
Furthermore, surface tensors satisfy the sum, product, and contraction properties. Finally, the
quotient theorem remains valid.
2.4The fundamental surface tensors
In this Section, we will continue following our Euclidean blueprint and introduce the covariant and
the contravariant bases and
,
the covariant and the contravariant metric tensors
and ,
the area element ,
and the Levi-Civita symbols
and .
2.4.1The position vector function
The position vector with an arbitrary origin is defined in the entire Euclidean
space. Naturally, the origin need not be on the surface. The
surface restriction of , i.e. the values of at points on the surface, can be thought of as a function of
the surface coordinates ,
i.e.
or, following our convention of
representing the collection of all independent variables by a single letter,
Suppose we fix the value of one of the coordinates, say , and
consider the function
By definition, traces out the coordinate corresponding to
the fixed value of and
varying .
Therefore, as we recall from Chapter TBD of Introduction to Tensor Calculus, the derivative
represents a tangent vector to that
coordinate line. This insight will help us with the geometric intuition of the covariant basis
which
we will now introduce.
2.4.2The covariant basis
Following the Euclidean blueprint, the covariant basis at a
given point is constructed by differentiating the
position vector function with respect to each of the surface
variables, i.e.
It is left as an exercise to
demonstrate that is a
tensor, i.e.
newline
Since the partial derivative
corresponds to the ordinary
derivative of the function , the covariant basis vector is
tangential to the coordinate line corresponding to varying and
fixed .
Similarly, is
tangential to the coordinate line corresponding to varying and
fixed .
Thus, both and
are
tangential to the surface and therefore represent a basis for
the tangent plane at . Thus, any vector
emanating from that lies in the tangent
plane, and no vector emanating from that lies outside of the
tangent plane, can be expressed in terms of .
For a vector in the tangent plane, the coefficients
in the linear decomposition
are referred to as the
contravariant surface components of . It is left as an exercise to show that
form a contravariant surface tensor.
Earlier in this Chapter, we agreed to accept the concept of the tangent plane without a definition.
However, we are now able to define the tangent plane at the point as the plane spanned by and
. Of
course, we must make sure that the resulting plane is invariant under a change of surface
coordinates. In other words, that all bases in all
coordinate systems
span one and the same plane. It is left as an exercise to show that this follows from the tensor
property of .
2.4.3The unit normal
Since the basis vectors span
the tangent plane, they are orthogonal to the unit normal , i.e.
Furthermore, recall the
normalization condition
The last two equations may be
adopted as the definition of the unit normal .
Observe that the above equations define to within direction. Indeed, if a vector satisfies these equations, then so does . One way to choose a unique normal is to
stipulate that the vectors , , and
form a positively-orientated set. In this approach, however,
flips under any change of coordinates that is not orientation
preserving. However, we would like to think of as an invariant and will therefore choose a unique according to other, coordinate-free, considerations.
2.4.4The metric tensors and
Once again following the Euclidean blueprint, the covariant metric tensor is
defined as the pairwise dot products of the elements of the covariant basis, i.e.
The covariant metric tensor is
symmetric, i.e.
and positive definite.
The area element is ,
where is the determinant of the matrix
associated with .
The determinant is a relative tensor of weight . Therefore, the area element
is a relative tensor of weight , albeit only with respect to orientation-preserving
coordinate changes.
The dot product of two tangent vectors and
is
given by
The length of a tangent vector is given by
The contravariant metric tensor
is the matrix inverse of ,
i.e.
where the Kronecker delta
is, of course, defined as
The metric tensors
and
can be used for index juggling in a way that is completely analogous to the Euclidean case.
For example, raising the subscript on a variant
results in a variant
with a superscript, i.e.
Similarly, lowering the superscript
on
results in a variant with a
subscript, i.e.
2.4.5The contravariant basis
The contravariant basis
is defined by the equation
Of course, we recognize it simply as
the operation of raising the subscript on the covariant basis .
It is left as an exercise to show that the vectors
are related to the covariant basis by
the identity
Furthermore, the covariant basis
can be
obtained from the contravariant basis
by lowering the index, i.e.
The components of a
tangent vector with respect to ,
i.e.
are known as the covariant
surface components of . They indeed form a covariant tensor and are related to the
contravariant components
by index juggling, i.e.
Furthermore, the contravariant components
of a vector in the tangent plane are given by the dot product
while the covariant components are
given by
2.4.6The Levi-Civita symbols
The definitions of the permutation systems
and
are precisely as described in Chapter TBD of Introduction to Tensor Calculus. Namely,
Similarly, the delta system
is the tensor product of two permutation systems, i.e.
Note that we will commonly make use
of the identity
In terms of the permutation systems,
the determinant of the covariant metric tensor is
given by the expression
The Levi-Civita symbols
and
are defined by the equations
The Levi-Civita symbols are tensors with respect to orientation preserving coordinate changes. They
can be used for a number of purposes including the definition of surface vorticity.
2.5Orthogonal projections onto and away from the tangent plane
Recall that a vector in the tangent plane can be represented by a linear
combination of the covariant basis vectors , i.e.
where the components
are given by
Meanwhile, a vector that does not lie in the tangent plane cannot be represented
by a linear combination of the vectors .
However, following the adage that all feasible tensor combinations are worthwhile, let us
investigate the geometric meaning of the combination
In other words, we will investigate
the geometric meaning of the vector
Of course, cannot equal since lies in the tangent plane while does not. However, as we are about to show, is the vector closest to among all vectors that lie in the plane. In other words,
is the orthogonal projection of onto the plane. Note that orthogonal projection was described
in Chapter TBD of Introduction to Tensor Calculus.
In order to demonstrate that is the orthogonal projection of , we must show that the difference is orthogonal to the tangent plane. Orthogonality to the
tangent plane is equivalent to orthogonality to each of the elements of the covariant basis or
contravariant basis .
The contravariant basis is more convenient for the present purpose. By dotting with ,
we find
Thus, is indeed orthogonal to and
therefore is indeed the orthogonal projection of onto the tangent plane.
Let us take a moment to admire the compactness of the formula
Recall that we have already
discussed the topic of the component space representation of orthogonal projection in Section TBD
of Introduction to Tensor Calculus Operating in a pre-tensor-notation context, we derived
the formula
A careful inspection of this equation will reveal that it represents the same computational
algorithm as its compact tensor counterpart.
Let us also admire the great universality of the formula
For a vector that lies in the tangent plane, this formula yields its
contravariant components. Meanwhile, for a vector that lies outside the tangent plane, it yields the
contravariant components of its orthogonal projection onto the plane, i.e. the vector in the plane
closest to .
Let us now turn our attention to projection away from the tangent plane, i.e. projection
onto the normal direction. By analogy with
consider the quantity
and the vector
The vector is the orthogonal projection of away from the surface if the difference is orthogonal to . To prove this, observe that
as we set out to show.
It is a geometrically obvious fact that a vector is the sum of its projections onto and away from
the tangent plane. In other words,
where parentheses are needed to
prevent the meaningless combinations and
. It is left as an exercise to demonstrate this
identity algebraically. In Chapter 3, this identity
will find a particularly elegant expression in terms of the ambient components.
2.6The surface Christoffel symbol
The first real and exciting difference between a Euclidean space and an embedded surface comes in
the definition of the Christoffel symbol .
Recall the definition of the ambient Christoffel symbol in
Chapter TBD of Introduction to Tensor Calculus:
The analogous definition
is
not possible on an embedded surface, since the vectors
may not lie in the tangent plane and can therefore not be expressed by linear combinations of . This
is a welcome development as it is the first instance of curvature making its presence felt.
Since curvature is a "second derivative" phenomenon, it is not surprising that it manifests itself
in the derivative of the covariant basis rather than the covariant basis itself.
At this point, we have two alternatives at our disposal for defining the Christoffel symbol. The
first is to imitate the explicit Euclidean formula
and thus to define
by the equation
The second alternative is to define
the Christoffel in terms of the derivatives of the metric tensor. In the context of a Euclidean
space, we showed that
Later on, in the context of Riemannian spaces in Chapter TBD of Introduction to Tensor
Calculus, we adopted the above equation as the definition of the Christoffel symbol.
Imitating this approach, known as intrinsic, we can define the
by the equation
Naturally, the intrinsic approach is more universal, as it can be extended to Riemannian spaces.
However, since we are pursuing a more geometric approach, we will choose the first definition, i.e.
The symbol
is sometimes referred to as the Christoffel symbol of the second kind. It is left as an
exercise to show that,
is symmetric in its subscripts, i.e.
satisfies the identity
and transforms according to the rule
under a change of surface
coordinates.
The Christoffel symbol of the first kind, ,
is obtained by lowering the superscript , i.e.
It is left as an exercise to show
that
and that
2.7Covariant differentiation of variants with surface indices
For a variant
with a representative collection of indices the definition of
reads
The flagship characteristic of is the
tensor property: if the input variant is a tensor, the output is also a tensor with an additional
covariant order. The covariant surface derivative satisfies the product rule, and commutes with
contraction.
In the case of the Euclidean space, we found that the covariant derivative kills
all metrics, i.e.
It is left as an exercise to show
that all but the first two analogous identities hold for the surface covariant derivative ,
i.e.
2.8The emergence of curvature
This is an exciting moment as we turn our attention to an analysis that brings out curvature.
Recall the metrinilic property of the ambient covariant derivative with
respect to ambient basis ,
i.e.
This property is easy to show since,
by definition, is
given by
and vanishes since the Christoffel symbol is given by
The same argument is not available on a surface. The covariant derivative of the covariant basis is
given by
However, the expression on the right
does not vanish since, as we discussed earlier, the combination lies
in the tangent plane while
may not -- due to curvature!
Nevertheless, the tensor
does have a special property -- each of its elements is orthogonal to the surface. In order
to show this, recall that
In order to take advantage of this
relationship, dot both sides of the identity
with :
The first term on the right equals
.
Meanwhile, for the second term, we have .
Thus the two terms cancel and we find
as we set out to show.
The object
has one additional special property. Namely, it is symmetric, i.e.
The proof of this identity is left
as an exercise.
As we have already observed, curvature is the very reason why
does not vanish. Therefore, the object
holds the key to quantifying curvature. We will now exploit this insight by introducing the
curvature tensor .
2.9The curvature tensor
We have just established that each element in the tensor is
orthogonal to the surface. Thus, each element is proportional to the unit normal . Denote by
the coefficients of proportionality between
and , i.e.
The object is
known as the curvature tensor. Its tensor property follows from the quotient theorem, as
well as from the fact that it can be expressed explicitly in terms of tensor quantities. Namely, by
dotting both sides of the above identity with the unit normal , we find that
Since is
symmetric, i.e.
the curvature tensor, too, is
symmetric, i.e.
Raising the index , we find
As discussed in Chapter TBD of
Introduction to Tensor Calculus, the system
does not correspond to a symmetric matrix. Nevertheless, since the systems
and
are related by the above identity, we can omit the dot placeholder and write the mixed curvature
tensor simply as .
Note that in the identity
the covariant derivative can be
replaced with the partial derivative, i.e.
This is so because
and therefore
Finally, since is orthogonal to , i.e.
, we arrive at the desired result
The advantage of this formula is
that it eliminates the need for the Christoffel symbol and thus simplifies the calculation of the
curvature tensor is some practical applications.
The invariant
known as the mean curvature,
is one of the most beautiful objects in our subject. Meanwhile, the determinant of ,
also an invariant, coincides with the Gaussian curvature as we described in the next
Section. The vector is
known as the curvature normal, another term that we have encountered before -- namely, in
Chapter TBD of Introduction to Tensor Calculus in the context of curves. The two definitions
of the curvature normal will also be reconciled in the future.
Finally, notice one important aspect of the curvature tensor evident in both of the equations
and
Namely, its values depend on the
choice of normal . If the opposite choice is made, then the values of curvature
tensor change their sign. Thus, the curvature tensor is defined with respect to a particular
choice of normal, and when we state the values of the elements of the curvature tensor, we must
specify which choice of normal it corresponds to. Of course, the same applies to the mean curvature
. On
the other hand, the Gaussian curvature, which is the determinant of
is insensitive to choice of normal since multiplying a matrix by does not change its determinant. Similarly, the
curvature normal is
insensitive to choice of normal since both terms in the product change sign when the choice of
normal is reversed.
2.10The surface Riemann-Christoffel tensor
As we mentioned earlier, another manifestation of curvature is the loss of commutativity for the
covariant derivatives. Recall that our proof of commutativity for the ambient covariant derivative
rested
on the availability of affine coordinates where the metric tensor is
constant from one point to another. Since we can no longer assume the availability of affine
coordinates, we can no longer expect that the surface covariant derivatives commute. This insight
opens a new avenue for the exploration of curvature. This avenue will be explored in Chapter 7. However, we will now mention some of the key
landmarks from that Chapter.
Following the Euclidean blueprint, we can show that for a first-order variant ,
the commutator
is given by
where
is the surface Riemann-Christoffel tensor given by
Since we cannot expect the surface
covariant derivatives to commute, the Riemann-Christoffel tensor generally does not vanish. It is
skew-symmetric in the first two indices, i.e.
the last two indices, i.e.
and is symmetric with respect to
switching the sets of the first two and the last two indices, i.e.
Owing to these symmetries, the
Riemann-Christoffel symbol in a two-dimensional space can be expressed by the equation
The invariant is known as the Gaussian
curvature. We have already encountered the concept of Gaussian curvature in the context of
Riemannian spaces in Chapter TBD of Introduction to Tensor Calculus. Curved surfaces are
thus breathing life into this concept and, indeed, that of a Riemannian space.
From the above equation, it follows immediately that is given explicitly by the equation
and, alternatively, by
The Riemann-Christoffel tensor is one of the central objects in the analysis of surfaces. One of
the highlights of our entire narrative will be the Gauss equations
which show that the
Riemann-Christoffel tensor can be obtained from the curvature tensor. Since, as we demonstrated in
Chapter TBD of Introduction to Tensor Calculus, the combination on the left is also given by
where is the determinant of the mixed
curvature tensor ,
we have
and therefore the Gaussian curvature coincides with , i.e.
The profound importance of these
identities will be discussed in Chapter 7.
2.11Weingarten's equation
We will now derive Weingarten's equation which is the formula for the covariant derivative
of the unit normal. It reads
Note, that since the unit normal
is a variant of order zero, its covariant derivative
coincides with its partial derivative, i.e.
It is not surprising to see the curvature tensor on the right side of Weingarten's equation since
it is curvature that is responsible for the variability in the unit normal . It is also not surprising that the result, being a linear
combination of the covariant basis vectors ,
is in the tangent plane. After all, has a constant length and, as we discovered in Section TBD of
Introduction to Tensor Calculus, constant length implies that the derivative is orthogonal
to the vector itself.
Since the unit normal is defined implicitly by the identities
our derivation of its covariant derivative will also be implicit. Let us start by applying
the covariant derivatives to both sides of the identity
By the product rule,
Since the two terms on the left are
equal, we find
This proves what we have already
anticipated, that is orthogonal to and therefore lies in the tangent plane.
Differentiating the identity
yields
According to the equation
the first term in the previous equation is precisely .
Therefore,
Raising the index yields
Recall that the contravariant
component
of a vector in the tangent plane is given by the dot product
Thus, the equation
tells us that the contravariant
component of the vector is . In
other words,
which is precisely Weingarten's
equation.
2.12The surface gradient, divergence, and Laplacian
For a scalar field defined on the surface, the vector
is referred to as the surface
gradient. To highlight its invariant nature, it may be denoted by the symbol , i.e.
although we will, of course, prefer
the indicial form. Much like its ambient counterpart, the surface gradient points in the direction
of the greatest increase in within the surface.
For a surface variant ,
the combination
is known as the surface
divergence. By the Voss-Weyl formula, it is given by
The differential operator
sometimes denoted by the invariant
symbol , is
known as the surface Laplacian, the Laplace-Beltrami operator, or simply the
Beltrami operator. It can be applied to a vector or a scalar field. An interesting
relationship that features the surface Laplacian applied to the position vector is
Its proof is left as an exercise.
By the Voss-Weyl formula, the surface Laplacian of a field is given by
2.13Planar curves
For a two-dimensional surface embedded in a three-dimensional Euclidean space, the concepts of the
unit normal and therefore that of the curvature tensor
rely on the fact that the surface is a hypersurface, i.e. its dimension trails that of the
ambient space by . A curve embedded in a Euclidean plane, known as a
planar curve, is also a hypersurface. Therefore, much of what we have already said about
surfaces can be extended to planar curves essentially without change.
Since curves are one-dimensional objects, Greek indices assume a single value of . Therefore, let us repeat what we have already said in
Section TBD of Introduction to Tensor Calculus. It may seem counterintuitive to use an index
that assumes a single value. You may think that it would be easier to denote the coordinate by
,
rather than ,
or to even drop the index altogether and denote it simply by . On the other hand, keep in mind that
the indicial signature tells us how the object transforms under a change of coordinates. Therefore,
preserving the indicial signatures is essential. Furthermore, indicial signatures inform us on how
to combine variants together to produce other meaningful variants. Finally, preserving the indicial
signatures will allow us to fit the theory of curves within the broader framework of embedded
surfaces. For all of these reasons, we will preserve the indicial signatures of all variants. Thus,
in a way, in this Chapter, we are aiming to take advantage of what curves have in common with
two-dimensional surfaces. By contrast, Chapter TBD of Introduction to Tensor Calculus and
Chapter 8 of this book exploit their
one-dimensional nature.
Let us now repeat the entire surface narrative for curves in minimal fashion and, along the way,
point out what remains exactly the same and what requires slight changes.
At each point, a planar curve is characterized by a unique tangent line.  (2.106) Furthermore, there is a unique direction orthogonal to the
curve, i.e. orthogonal to the tangent line. Therefore, there are two unit normals pointing in
opposite directions. The symbol represents the unit normal, in the sense that one of the two
unit normals is chosen arbitrarily.
(2.106) Furthermore, there is a unique direction orthogonal to the
curve, i.e. orthogonal to the tangent line. Therefore, there are two unit normals pointing in
opposite directions. The symbol represents the unit normal, in the sense that one of the two
unit normals is chosen arbitrarily.  (2.107)
(2.107)
 (2.106)
(2.106) (2.107)
(2.107)The covariant basis ,
defined by the equation  (2.108) The covariant metric tensor
(2.108) The covariant metric tensor
consists of a single vector that
points in the tangential direction.
 (2.108)
(2.108)
consists of a single element that equals length squared of the basis vector . The
line element
equals the length of the basis vector.
The contravariant metric tensor
can still be defined by the identity
Of course, in actuality, its only
element is the reciprocal of the length squared of . The
contravariant basis vector
is given by
It points in the exact same
direction as and
its length equals the reciprocal of the length of .
The permutation systems and
each have one index and a single entry that equals . The Levi-Civita symbols and
are defined by the equations
and each has a single element:
and .
The Levi-Civita symbols are tensors with respect to orientation-preserving coordinate changes.
The entire machinery of Tensor Calculus continues to work. An unusual invariant not available in
higher dimensions is . It
corresponds to the unit tangent vector that points in the same direction as .  (2.112) Much like ,
is an invariant only with respect to orientation-preserving
coordinate changes. Indeed, we know that changes the direction when the orientation of the
parameterization of the surface is reversed. Thus, its not an invariant in the full tensorial
sense: the orientation-preserving stipulation is necessary.
(2.112) Much like ,
is an invariant only with respect to orientation-preserving
coordinate changes. Indeed, we know that changes the direction when the orientation of the
parameterization of the surface is reversed. Thus, its not an invariant in the full tensorial
sense: the orientation-preserving stipulation is necessary.
 (2.112)
(2.112)This is a good moment to draw your attention once again to the elegance of Tensor Calculus. In
Chapter TBD of Introduction to Tensor Calculus, the unit tangent was introduced as the derivative of the position vector with respect to the arc length. If the curve is referred to
any other parameter then, in the absence of the tensor
framework, the only way of arriving at is to divide by its length:
Now, compare the above calculation
to the tensor alternative
I feel very strongly that the tensor
expression is more elegant.
For the Christoffel symbol ,
we once again use the geometric definition
Of course, it has only a single
element .
The value of this element can be determined from the equation
which follows from the definition.
Let denotes the length of the covariant basis
vector as a
function of the coordinate ,
i.e. ,
then the single element of the Christoffel symbol equals
The Riemann-Christoffel tensor
is given by  (2.118) When the curve is related to the arc length , i.e. , the resulting covariant basis vector is
length at all points. As a result, the covariant metric tensor
has the constant value of . Consequently, the Christoffel symbol vanishes
identically and, with it, so does the Riemann-Christoffel tensor. An important consequence of this
insight is the fact that covariant derivatives commute, i.e.
(2.118) When the curve is related to the arc length , i.e. , the resulting covariant basis vector is
length at all points. As a result, the covariant metric tensor
has the constant value of . Consequently, the Christoffel symbol vanishes
identically and, with it, so does the Riemann-Christoffel tensor. An important consequence of this
insight is the fact that covariant derivatives commute, i.e.
However, in contrast with
two-dimensional surfaces, the Riemann-Christoffel tensor on a one-dimensional curve does vanish,
i.e.
This follows from the availability
of a perfectly regular coordinate system that we utilized so effectively in Chapter TBD of
Introduction to Tensor Calculus -- namely, the arc length .
 (2.118)
(2.118) on curves.
In Chapter 7, we will discover that this is a
special case of a more general fact: the Riemann-Christoffel tensor vanishes on all surfaces that
can be "straightened out" isometrically, i.e. without altering distances between points. Any
two-dimensional surface, that can be made out of a sheet of paper by gently curving it without
stretching or shrinking, i.e. isometrically, has this property. Such surfaces can just as easily be
straightened back out isometrically. Special surfaces that have this property include cylinders and
cones. Similarly, any curve that can be formed out of a string without stretching or shrinking,
i.e. isometrically, has this property, as well. But that, of course, is all curves.
The curvature tensor is
defined in the same way as for two-dimensional surface:
In the context of curves embedded in
the plane, the mean curvature may
be referred to simply as curvature. The vector is
the curvature normal.
Note that the new definitions of the curvature and the curvature normal are in exact
agreement with the concepts of the signed curvature and the curvature normal that were introduced in Chapter TBD of Introduction to
Tensor Calculus, where the entire analysis was based on parameterizing the curve by its arc
length . Despite the different approaches, the equivalence
between the old and the new definitions is made obvious by the Tensor Calculus framework. The
objects and
are
invariants and therefore yield the same value regardless of the chosen parameterization. At
the same time, under the arc-length parameterization, i.e. , the curvature normal becomes
which coincides with
Naturally, the same argument proves
that the mean curvature and
the signed curvature are one and the same thing.
2.14Exercises
Exercise 2.1Show that surface tensors satisfy the sum, the product, and the contraction properties.
Exercise 2.2Show that surface tensors satisfy the quotient theorem.
Exercise 2.3Show that the surface tensor property is reflexive, symmetric, and transitive.
Exercise 2.4Show that
Exercise 2.5Show that
Exercise 2.6Show that the covariant components of a vector in the tangent space are given by
Exercise 2.7Demonstrate the equation
algebraically. To this end, note that the set of vectors , , and represents a basis for the three-dimensional space and show that the two vectors on both sides of the equation produce the same values when dotted with each element of the basis.
Exercise 2.8Show that
Exercise 2.9Show that
implies that
Exercise 2.10Show that
Exercise 2.11Show that is metrinilic with respect to the covariant metric tensor , i.e.
Exercise 2.12Show that is metrinilic with respect to the Kronecker delta , i.e.
Exercise 2.13Show that is metrinilic with respect to the contravariant metric tensor , i.e.
Exercise 2.14Show that is metrinilic with respect to the Levi-Civita symbols, i.e.
and
Exercise 2.15Show the symmetry of the object , i.e.
Exercise 2.16Show that
and
These identities will prove useful on a few occasions.
Exercise 2.17The Riemann-Christoffel tensor with all subscripts is given by . Show that
Exercise 2.18Show that the covariant derivatives commute when applied to a variant of order zero, i.e.
Exercise 2.19Show that the Laplacian of the position vector is given by
Exercise 2.20Construct an alternative narrative where Weingarten's equation
is adopted as the definition of the curvature tensor from which the equation
follows as a corollary.
Exercise 2.21For a two-dimensional surface, show that if is chosen so that the set is positively oriented, then
Exercise 2.22For a two-dimensional surface, show that the normal is given by the identity
and that the resulting normal is such that the set is positively oriented. Of course, the above identity is simply the elegant tensor version of the formula
found in elementary textbooks.
2.14.1The Gauss equations of the surface
Over the next three exercises, we will derive the celebrated Gauss equations of the surface
along with the equally elegant Codazzi equations
begin{exercise} Show that for the commutator applied to a surface covariant
tensor ,
we have
In particular,
end{exercise}
Exercise 2.23Show that
Thus,
Exercise 2.24From the above equation, derive the Codazzi equations
as well as the identity
Finally, show that this identity is equivalent to the Gauss equations of the surface