In this Chapter, we will calculate the fundamental variants introduced in the previous Chapter --
the shift tensor , the
metric tensors
and ,
the area element ,
the components of
the unit normal, and the Christoffel symbol
-- for concrete surfaces. Examples always bring theory to life but, in the case of surfaces, they
are particularly important: while all Euclidean spaces are essentially the same, each surface
represents its own unique space.
4.1A sphere of radius
We will begin with a sphere of radius referred to coordinates illustrated
in the following figure. 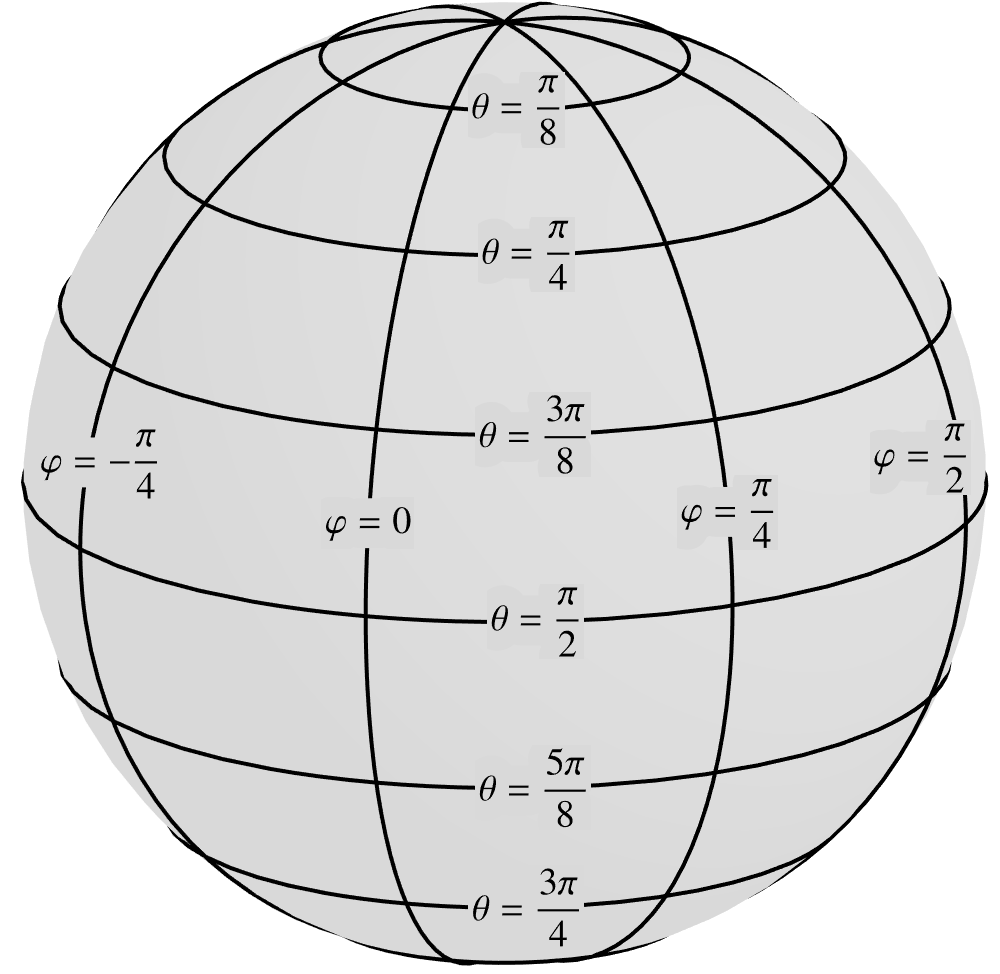 (3.7) This example will offer a great deal of insight as we will
analyze it with the help of two different ambient coordinate systems: Cartesian and spherical.
Since a spherical coordinate system is perfectly suited to the geometry of a sphere, its use will
simplify our calculations despite the greater complexity of the ambient metric tensor and
Christoffel symbol.
(3.7) This example will offer a great deal of insight as we will
analyze it with the help of two different ambient coordinate systems: Cartesian and spherical.
Since a spherical coordinate system is perfectly suited to the geometry of a sphere, its use will
simplify our calculations despite the greater complexity of the ambient metric tensor and
Christoffel symbol.
 (3.7)
(3.7)In this Chapter, we will denote matrices corresponding to a system by putting brackets around the
associated indicial symbol. For example, will denote the matrix
associated with the covariant metric tensor and will denote the matrix corresponding to the
shift tensor.
4.1.1In Cartesian ambient coordinates
Let us operate with spherical coordinates on the surface and Cartesian coordinates in the ambient space. Recall the
equations of the surface
Recall that all versions of the ambient metric tensor, i.e. ,
,
and ,
correspond to the identity matrix, i.e.
Thus, the placement of the
ambient indices has no effect on the values of any of the variants.
The shift tensors and
are
obtained by differentiating the equations of the surface with respect to each of the surface
variables, and . Therefore, we have
The covariant metric tensor is
given by the equation
and is therefore represented by the
matrix
which yields
Since is diagonal, the covariant basis
is orthogonal. Also, you probably recognize as the bottom right submatrix of the metric tensor associated with spherical
coordinates in a three-dimensional Euclidean space. It is left as an exercise to explain why this
is so by observing the relationship between and
the ambient covariant basis corresponding to spherical coordinates.
The contravariant metric tensor
corresponds to , i.e.
The area element
is the square root of the determinant of , i.e.
If you recall,
is used in converting geometric integrals over the surface into arithmetic integrals. For example,
the total area of the sphere of radius is given by
Next, let us calculate the shift tensors
and
with raised surface indices. Since,
we have
where justifying the order of the terms in the matrix products is left as an exercise. Note that,
technically, the above products should involve ,
however the transpose is not necessary since is symmetric. Carrying out the matrix products,
we find
Let us now turn our attention to calculating the components of
the unit normal. This can be accomplished in two ways. First, recall the normalization condition
which, in matrix form, reads
It tells us that is contained in the null space of the matrix
.
Thus, can be calculated by determining the null space
of
and then normalizing it to unit length. It is left as an exercise to show that the transposes of
the matrices corresponding to all four forms of the shift tensor, i.e. ,
, ,
and ,
have the same null space. Furthermore, calculating by
this approach is also left as an exercise.
Second, the components can
be calculated by evaluating the cross product of the vectors and
, once
again followed by normalization to unity. As we discussed in Chapter 3, the components of and
are
contained in the columns of the matrix
In anticipation of the normalization
step, we can drop the factors of from in the cross product
calculation. Therefore, we have
The length of the resulting vector is . Thus, dividing by , we find
or
Finally, note that for a sphere, the
components could
have also been easily guessed from geometric considerations as we know that is a unit vector pointing in the radial direction and is
therefore collinear with the position vector if the latter emanates from the center of the sphere.
The last remaining object to be calculated is the surface Christoffel symbol .
Recall that the relationship between the surface and the ambient Christoffel symbols reads
which reduces to
when the ambient space is referred
to affine coordinates, which is the case here. The above identity has three free indices , , and and, therefore, cannot be captured by
a matrix identity. In order to continue using matrix algebra, we need to fix the value of one of
the free indices. We will choose for this role and consider and separately. Since and , we have
The elements of are obtained by
differentiating with respect to , i.e.
Since
we find
Meanwhile, the elements of are obtained by differentiating with respect to , i.e.
As before, since
we find
In summary, the three nonzero elements of
are
This completes our analysis of a sphere of radius in Cartesian ambient coordinates. We
will now repeat the same analysis in spherical ambient coordinates and it will be particularly
interesting to observe what changes and what stays the same.
4.1.2In spherical ambient coordinates
Let us now perform the parallel analysis using the same coordinates on the surface and spherical coordinates in the
ambient space. Recall that for this combination of coordinate systems, a sphere of radius is described by the exceedingly
simple equations
The ambient covariant metric tensor ,
on the other hand, is more complicated than in the case of Cartesian coordinates. It was calculated
in Section TBD of Introduction to Tensor Calculus where we showed that it corresponds to the
matrix
Thus, the contravariant metric
tensor
corresponds to
The shift tensor is
obtained by differentiating the equations of the surface with respect to and and has the exceedingly simple form
Since the metric tensor does not correspond to the
identity matrix, the shift tensor
corresponds to a different matrix compared to .
Since
we have
which yields
The covariant metric tensor is
related to the shift tensors and
by the equation
Therefore, we have
Crucially, we have arrived at the
same values as before. This is entirely to be expected since
does not depend on the choice of the ambient coordinates. Thus, the contravariant metric tensor
and the area element
also have the same value as before and need not be documented here.
Now we can calculate the two remaining forms of the shift tensor. The contravariant form
is given by
and therefore corresponds to the matrix product which yields
Finally, is
given by
and therefore corresponds to the product which yields
It is interesting to note that and
have identical values, which is not true in general. It is left as an exercise to explain why it
makes sense in this case by considering the relationships between the contravariant surface and
ambient space bases.
The components of
the normal are, once again, easy to guess, since the (exterior) unit normal coincides with the ambient basis vector
Therefore, the components are
given by
Note that this result could have
also been obtained either from the null space of the matrix
or by calculating the cross product
of and
.
Finally, although we already know the elements of the Christoffel symbol ,
it will be interesting to calculate them again since this time, it is the first term on the
right in the identity
that survives. Indeed, the second
term vanishes since the elements of the shift tensor are
constants. Therefore, we have
Once again, matrix algebra cannot capture all aspects of the above identity. We therefore again
have to fix the values of some of the indices. Let us choose and consider and separately. For , we have
while for , we have
Recall that
Thus, the only nonzero element in
is and the only nonzero element of
is . Thus expressions for
and
are given by the simplified equations
which can be handled by matrix algebra. Recall that the nonzero elements of the ambient Christoffel
symbol
are
Organize the values of the systems
and on
the surface of the sphere into matrices, i.e.
With the help of these matrices, we have
and
Collecting the nonzero elements of ,
we observe that we have arrived at the same values as before, i.e.
This completes our analysis of a sphere of radius .
4.2A cylinder of radius
Consider a cylinder of radius referred to coordinates illustrated in the following figure.
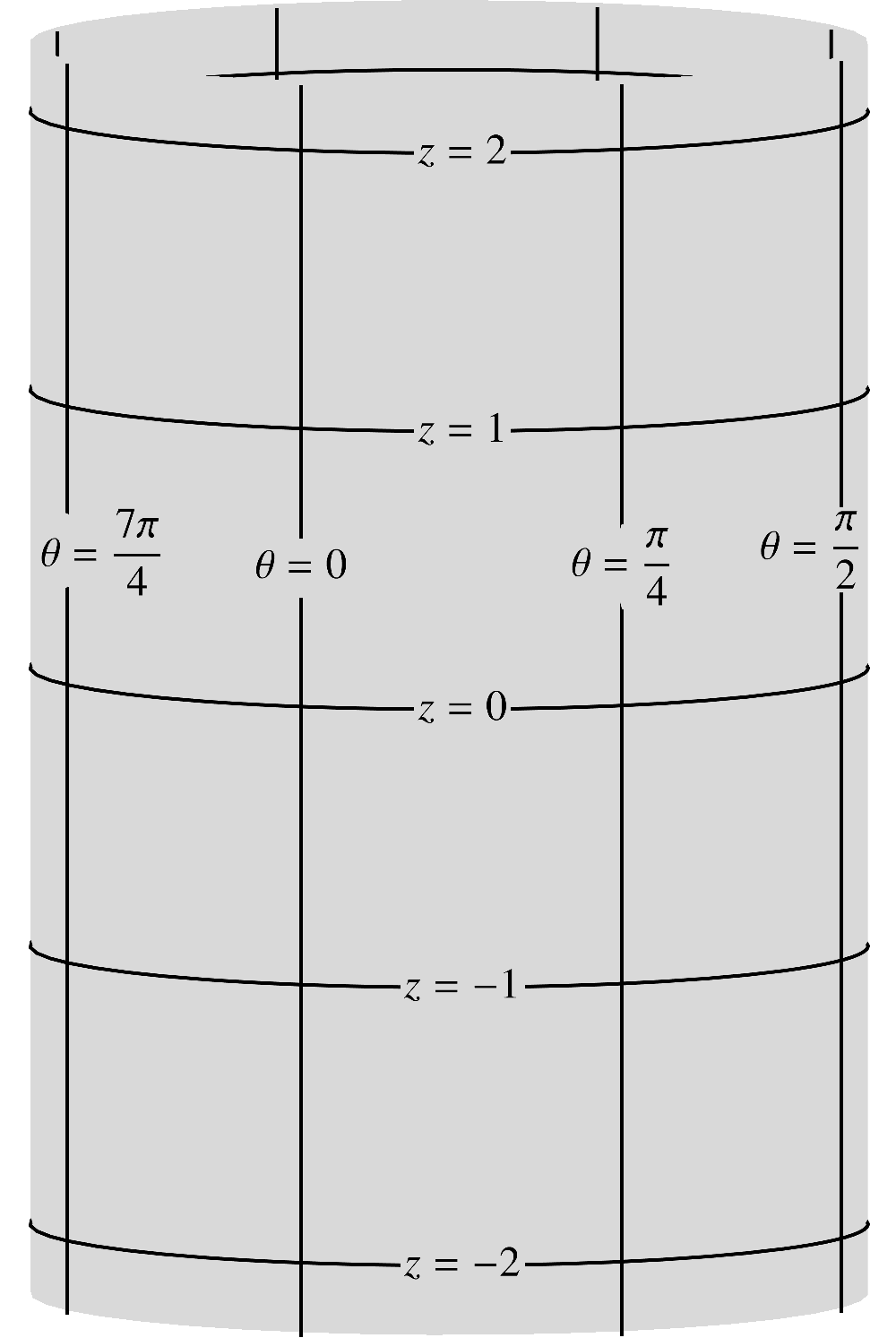 (3.14) As was the case with a sphere, a
cylinder can also be effectively analyzed by referring the ambient space either to Cartesian or
cylindrical coordinates. We will choose Cartesian coordinates and
save cylindrical coordinates for the exercises. Recall that the equations of the surface read
(3.14) As was the case with a sphere, a
cylinder can also be effectively analyzed by referring the ambient space either to Cartesian or
cylindrical coordinates. We will choose Cartesian coordinates and
save cylindrical coordinates for the exercises. Recall that the equations of the surface read
 (3.14)
(3.14)
Once again, the ambient metric tensors
and
corresponds to the identity matrix
and thus, once again, the placement
of the ambient indices has no effect on the values of any of the variants.
The shift tensors and
are obtained by differentiating the equations of the surface with respect to and , which yields
The surface metric tensor is
given by
and therefore
while
The area element
is the square root of the determinant of , i.e.
Notice that the elements of the metric tensors have constant values, which is a signature feature
of affine coordinates. The fact that a cylinder admits such a coordinate system distinguishes it
from all the other two-dimensional surfaces discussed in this Chapter. This fact means that, in a
certain sense, a cylinder represents a Euclidean space. On the one hand, this makes sense, since a
cylinder can be cut along a line of constant and uncurled, without any distortion,
into a flat strip. On the other hand, a cylinder is a curved surface that cannot accommodate
straight lines, except in one special direction. Understanding this dichotomy will be one of the
goals of our study of curvature.
Let us now return to the calculation of the remaining differential objects. The shift tensors
and
correspond to the matrix product which yields
As was the case with the sphere, the components of
the unit normal can be determined from the null space of , by calculating the cross
product of and
, or
simply by intuiting from general geometric considerations. In any case, the components
correspond to the matrix
Since the elements of the metric
tensors are constant, the Christoffel symbol
vanishes at all points, i.e.
which can also be described as a
signature characteristic of an affine coordinate system.
This completes our analysis of a cylinder and we will now turn our attention to the more general
surfaces of revolution.
4.3Surfaces of revolution
A sphere and a cylinder are both examples of surfaces of revolution. Thus, the analysis presented
in this Section represents a generalization of the preceding two Sections. 
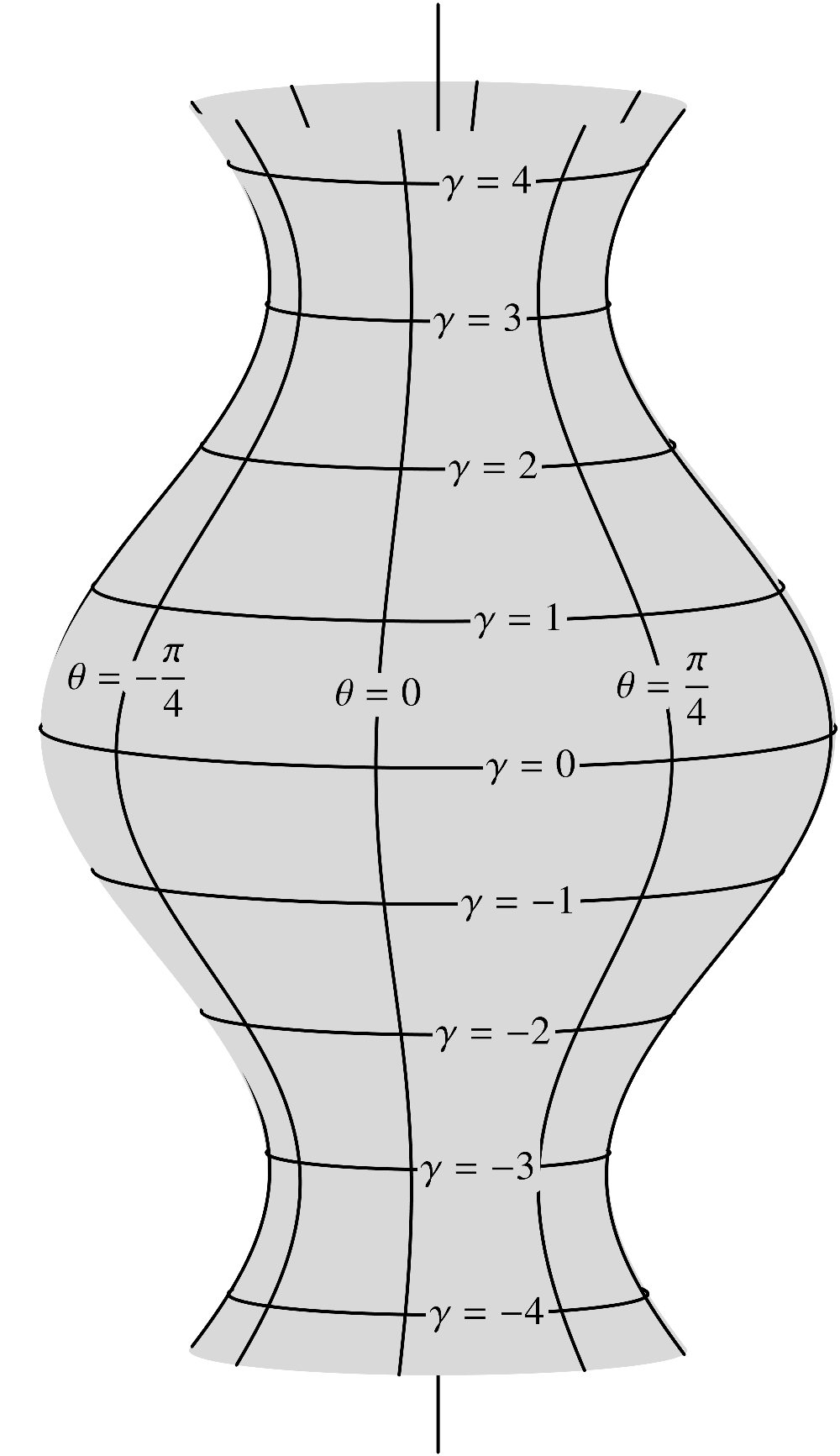 (3.21)
(3.21)

 (3.21)
(3.21)We will refer the ambient space to Cartesian coordinates and will invite the reader to repeat the
analysis in cylindrical coordinates as an exercise. In Cartesian coordinates , the equations of a surface of
revolution read
Since we have already performed several similar analyses, we will begin to omit some of the details
in the upcoming calculations. Filling in those details will be left as exercises.
The shift tensors and
are
obtained by differentiating the equations of the surface with respect to and , which yields
where
and
denote the derivatives of the functions and .
For the covariant and the contravariant metric tensors, we have
The area element
is given by
For the remaining forms
and of
the shift tensor, we have
For the components of
the normal, which can be determined by any of the approaches described above, we have
The nonzero elements of the Christoffel symbol
are
The findings of this Section will pay instant dividends as we turn our attention to another shape
of revolution: a torus.
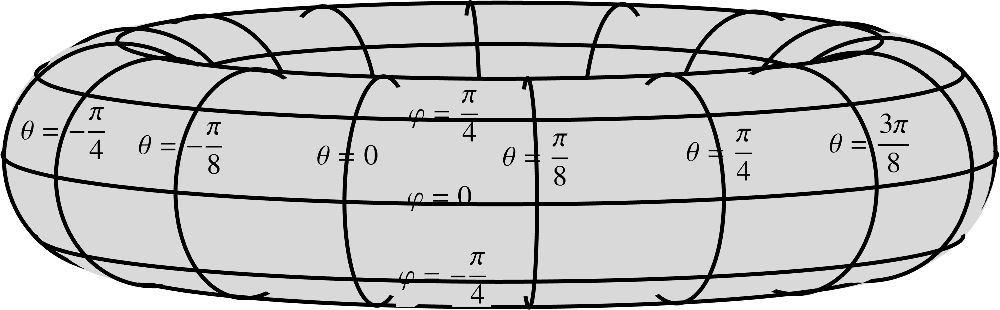
4.4A torus with radii and
A torus with radii and is a shape of revolution obtained by
rotating a circle of radius around an axis that is a distance
from the center of the circle. Note
that, unlike other Sections where the symbol denotes one of the ambient
coordinates, in this Section, is a constant parameter.  (4.67) Within its plane, the circle is described by the equations
(4.67) Within its plane, the circle is described by the equations
 (4.70) When the ambient space is referred to
Cartesian coordinates , the equations of the torus read
(4.70) When the ambient space is referred to
Cartesian coordinates , the equations of the torus read
 (4.67)
(4.67)
The following figure illustrates the resulting surface coordinates and . Note that both coordinates vary from to .
 (4.70)
(4.70)
All of the following identities can be obtained as special cases of the equations from the previous
Section on surfaces of revolution. Therefore, we will catalogue the results without further
clarifications.
The shift tensors and
:
The metric tensors
and ,
and the area element :
With the help of the area element ,
we can calculate the total area of the torus, i.e.
The shift tensors
and :
The components of
the normal:
And, finally, the nonzero elements of the Christoffel symbol :
This completes our analysis of two-dimensional surfaces embedded in a three-dimensional Euclidean
space and we now turn our attention to curves in a two-dimensional Euclidean plane.
4.5Planar curves
The theory that we have developed for surfaces applies, without any changes, to one-dimensional
curves in a two-dimensional Euclidean plane. In fact, with the exception of the normal which
requires the surface to be a hypersurface, all of the fundamental differential objects considered
in this Chapter can be calculated for a curve embedded in a space of any dimension. We will,
however, limit ourselves to curves in the plane here, and save the study of curves in a
three-dimensional space for Chapter 8.
4.5.1In Cartesian coordinates
A one-dimensional curve is parameterized by a single coordinate which
we will denote by the letter . First, refer a two-dimensional plane
to Cartesian coordinates and consider a general curve given by
the equations
In the equations that follow, the symbols and will refer to the functions and while ,
,
,
and
will refer to the derivatives , , , and .
The ambient metric tensors
and
correspond to the identity matrix, i.e.
The shift tensors and
are
obtained by differentiating the equations of the curve with respect to , i.e.
The surface metric tensor
corresponds to the matrix product . The result is a matrix with a single entry. Nevertheless, we will
continue to use brackets to denote the matrices. We have
The contravariant surface metric
tensor
is the matrix inverse of .
Since is a matrix, its inverse consists of a single entry that is
the reciprocal of the sole entry in , i.e.
The determinant of the matrix equals its only entry.
Therefore, the length element
is given by the equation
This is a familiar expression that
we have encountered on numerous occasions when studying curves.
The remaining forms of the shift tensor are
The single entry of the Christoffel symbol
is given by
Finally, the components of the normal are given by
Let us now catalogue the values of the same objects for two special parameterizations. In the first
one, use the arc length for the coordinate along the curve. Recall that
represents a unit tangent
vector. Since, and represent its components, we
have
This identity leads to the
simplifications found in the following table.
For the second special case, consider a curve given by the graph of a function . Recall that such a curve is
described by the parametric equations
Using in place of , we have the results summarized in
the following table.
4.5.2In polar coordinates
Now, suppose that the plane is referred to polar coordinates . A general curve is given by the
parametric equations
In the equations that follow, the symbols and will refer to the functions and while ,
,
,
and
will refer to the derivatives , , , and .
The matrices corresponding to the ambient covariant and contravariant metric tensors
and
are
For the shift tensor and
, we
have
For the surface metric tensors
and ,
we have
The line element
equals the sole entry of , i.e.
For the remaining forms
and of
the shift tensor, we have
The Christoffel symbol
has the single entry
Finally, for the components of
the normal, we have
Let us again catalogue the same two special cases as in the case of Cartesian ambient coordinates.
First, refer the curve to arc length . In terms of the symbols and , the above expressions simplify
to the following:
Finally, for a curve that represents the graph of a function , we have
4.6Exercises
Exercise 4.1Calculate all forms of the shift tensor and the covariant metric tensor for a sphere of radius described in cylindrical ambient coordinates by the equations
Confirm that agrees with our earlier analyses.
Exercise 4.2Calculate all forms of the shift tensor and the covariant metric tensor for a cylinder of radius described in cylindrical ambient coordinates by the equations
Confirm that agrees with our earlier analyses.
Exercise 4.3Calculate all forms of the shift tensor and the covariant metric tensor for a cylinder of radius described in spherical ambient coordinates by the equations
Confirm that agrees with our earlier analyses.
Exercise 4.4Explain why the transposes of the matrices and have the same null space.
Exercise 4.5Calculate the components of the unit normal to the sphere of radius by finding a nonzero vector in the null space of the matrix
and normalizing it to .
Exercise 4.6Use matrix algebra to calculate the elements of the surface Christoffel symbol on the sphere of radius by considering the cases and separately.
Exercise 4.7Use matrix algebra to calculate the elements of the surface Christoffel symbol on the sphere of radius by considering the cases and separately.
Exercise 4.8Fill in the details of the calculation in Section 4.3.
Exercise 4.9Repeat the calculation in Section 4.3 in cylindrical ambient components.
Exercise 4.10Derive the equation
in two ways. First, by utilizing the formula
and, second, by utilizing the formula
Exercise 4.11Repeat the previous exercise for the equation
except note that, in this case, you will need to use the equation
Exercise 4.12Show that the surface Laplacian on a sphere with radius is given by
Exercise 4.13Show that the surface Laplacian on a cylinder with radius is given by
Exercise 4.14Show that the surface Laplacian on a torus with radii and is given by
Exercise 4.15Show that the surface Laplacian on the surface of a revolution whose profile is described by a function is given by